從以往的仿真經驗來看，單相逆變器仿真是一個簡單、不需要太多計算與調試就可以實現基本正弦波的輸出。如果輸出電壓不理想，調整調整載波頻率、電感、電容也可以勉強的輸出正弦波。但是當涉及到逆變器的閉環控制、三相逆變器的開環閉環仿真時，會發現調試變得困難，瞎湊參數也湊不出理想的波形。復雜一些涉及到并網逆變器、直接功率控制等控制方法的仿真更是難上加難。此時就會想到數學模型的魅力。根據計算的數學模型、傳遞函數、設計閉環環路控制才是王道。因此從簡單的單相逆變器重新開始學習。本次學習不注重逆變器原理的仿真，主要學習一些關鍵公式的推到，并通過仿真的形式驗證關鍵公式。

1 單相逆變器的基本原理

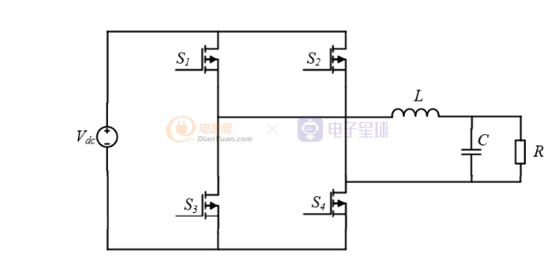
簡單介紹一下工作原理：

在SPWM調制下，1、4互補導通，2、3互補導通。1、4導通輸出+Vdc，2、3導通輸出-Vdc。14、23導通時間由SPWM調制計算得出。所以可以將你便電路進行簡化，簡化電路如下：

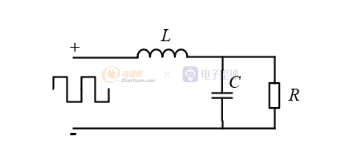
可以把逆變電路分為兩個部分。1 SPWM波產生電路  2 LC濾波電路

SPWM波產產生的是方波，逆變電路想要輸出的是一個正弦波。兩者除了在波形上有差距，最本質的差距就是方波內包含想要輸出的正弦波以及不想要輸出的雜波。這個雜波就是諧波。

LC濾波器，就起到把其余雜波濾掉的功能，同時不能濾掉我們希望得到的波形。

所以就需要搞清楚三個問題。

1 我們想要輸出的正弦波是什么。如何確定SPWM方波內包含期望輸出的正弦波？

2 SPWM方波內除了期望的正弦波，還包含什么樣的波？

3 LC濾波器能濾除什么樣的波？

問題1：

SPWM調制的原理：將期望輸出電壓作為調制波，將高頻三角波作為載波，將調制波與載波進行比較。當調制信號大于載波信號時，逆變器輸出電壓為正，當調制信號小于載波信號時，逆變器輸出電壓為負。這個過程就是調制。PWM調制的基礎原理：對于具有慣性的環節而言，如果多個窄脈沖的面積（沖量）相等，即使它們的形狀不同，這些窄脈沖加在環節上的效果也是基本相同的。

通過PWM調制就可以將調制波這個模擬信號轉化為數字信號。模擬信號就是一個連續的波形。而轉化呈的數字信號是一個僅包含0 1的信號，表現形式就是一個方波。而方波的脈沖的寬度就包含著那個模擬信號的信息。我們調制波為我們期望輸出的波形，SPWM調制出來的SPWM方波內就包含著我們期望輸出波形。

 問題2 

SPWM方波的諧波含量。

根據傅里葉變換可知，每一個周期性的信號，都是由不同頻率、幅值、相位的正弦波組成。因此可以根據傅里葉的理論分析出SPWM波內的波形組成，這個過程就是傅里葉變換。傅里葉變換可以通過傅里葉展開式計算，（我也嘗試學著推到SPWM方波傅傅里葉展開式，但沒有找到具體的推導過程。自我感覺就算找到也不理解），本文不對詳細推導過程做過多闡述，僅借用文獻[1][2]的結果 ，后續將通過仿真全方面驗證SPWM方波的諧波含量。

文獻[1]基于MATLAB的單相SPWM逆變電路諧波分析-付江夢

文獻[2]SPWM單相逆變電路的諧波分析-胡賽純