電源工程師對于開關電源峰值電流型控制都比較熟悉,由于峰值電流型小信號精確模型的傳遞函數比較復雜,所以對于環路穩定性的設計一般都采用仿真的方法。筆者試圖通過建模,用解析的方法來分析環路的穩定性,然后闡述電流內環參數的選擇對電壓外環的影響。
對于開關電源峰值電流型反饋控制系統的精確建模,張衛平教授在他的著作《開關變換器的建模與控制》一書中,已經給出了完整的推導過程,這里筆者就不再贅述了,感興趣的讀者可以自行查看該書(新版)的第6章節的內容(從186頁到226頁)。該書推導了從控制電壓Vc(s)到占空比d(s)的這一環節的傳遞函數,但沒有進一步論述外部的電壓環路傳遞函數和斜率補償對電壓環路穩定性的影響。筆者就在張衛平教授推導模型的基礎上,再推導完整的峰值電流型傳遞函數。接下來以BUCK電路為例說明,下圖為張教授推導的峰值電流型控制的小信號模型(時域下)。
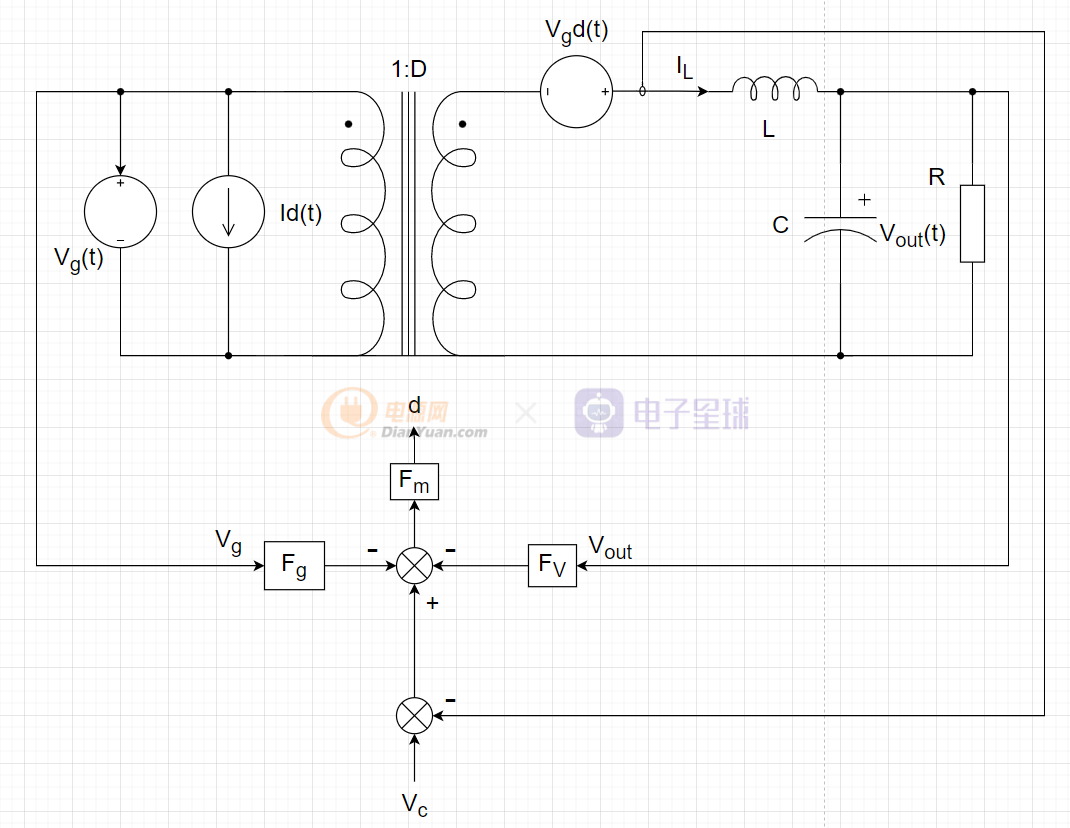
其中,
,
D為占空比直流量,d(t)為占空比小信號擾動,Ts為PWM的開關周期,L為電感量,Ma為斜率補償系數。
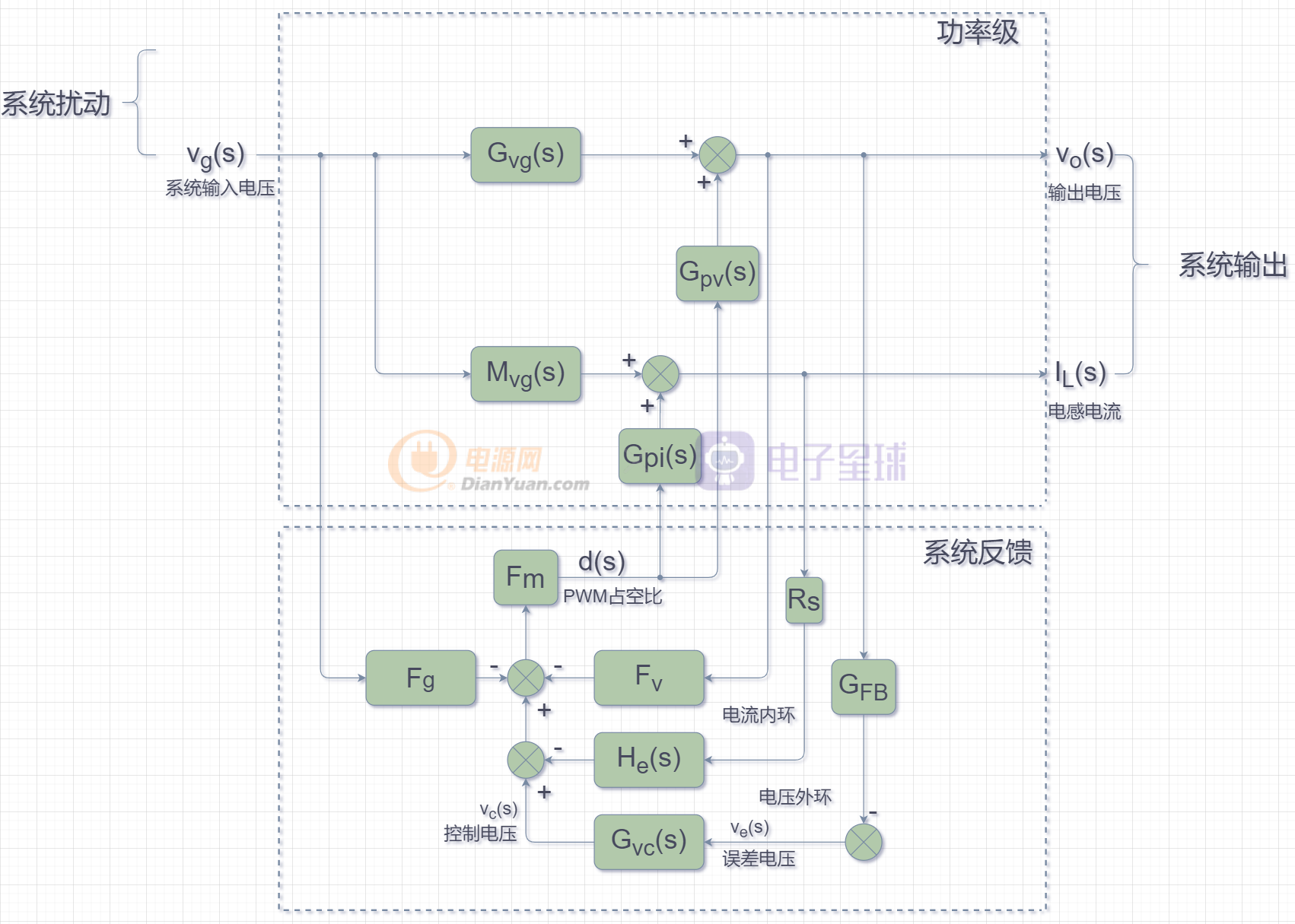
以上面的模型為基礎,再添加上輸出電壓及電感電流的反饋、占空比d(s)對輸出電壓和電感電流的控制,從而得出通用開關電源電路的拉氏變換控制系統框圖如下:

上圖中有兩點需要說明一下:
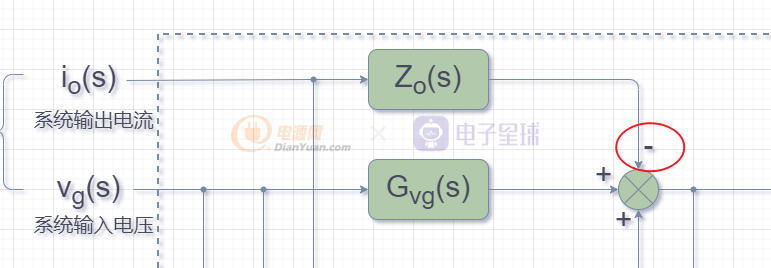
因為輸出電流io(s)的增加,會引起輸出電壓Vo(s)的下降(電源輸出阻抗),所以上圖中的紅圈為負。
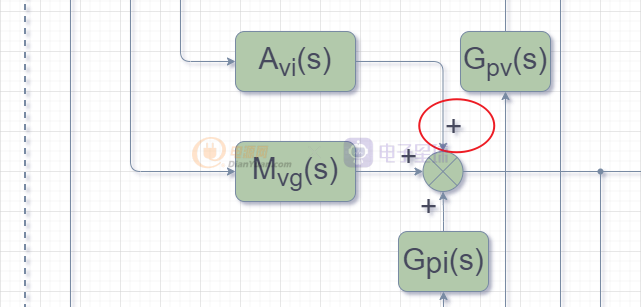
因為輸出電流io(s)的增加,會引起電感電流IL(s)的增加,所以上圖中的紅圈為正。
在功率級框圖中,系統的輸入電壓和輸出電流做為系統的擾動,輸出電壓和電感電流做為系統的輸出,輸出電壓設定(Vref)做為控制系統的輸入,d(s)占空比分別控制輸出電壓和電感電流。上圖中的綠色方框部分有的已經建模得到了相關的傳遞函數,剩下沒有建模環節的傳遞函數將通過下面的推導得出。
通過對開關量進行小信號線性等效,并將元器件中的寄生參數考慮進去(Re為電感的等效電阻,Rc為電容的等效串聯電阻,RL為負載電阻),可以得到如下的BUCK變換器的模型(s域):
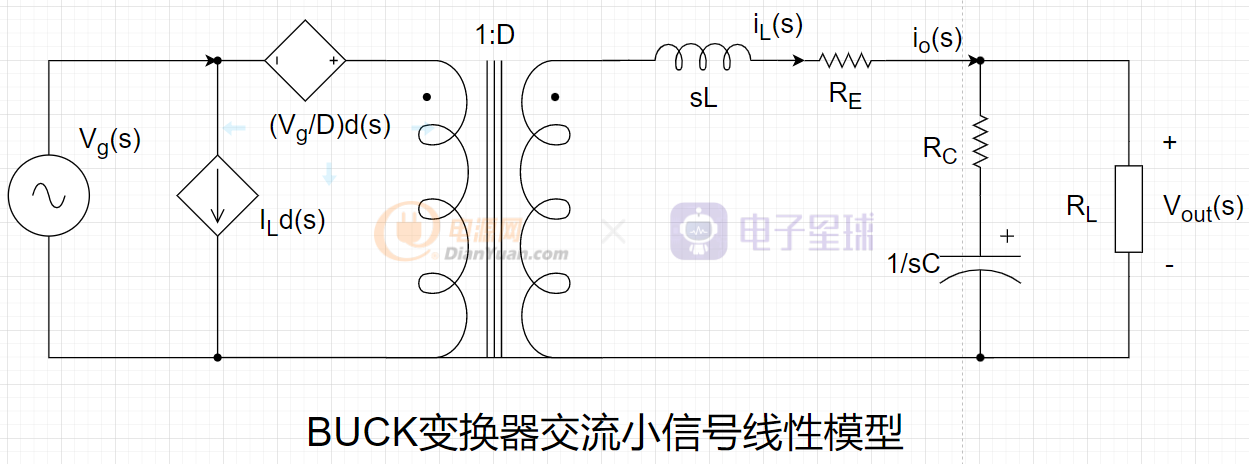
Vg表示直流量,Vg(s)表示小信號交流量。同理D表示直流量,d(s)表示小信號交流量,電路中其它變量交直流量表示方法也相同。
1)求Gvg傳遞函數
表示Vg(s)單獨影響Vo(s),所以要將d(s)置零并將io(s)對Vo(s)的影響忽略,從而得到下面的框圖:
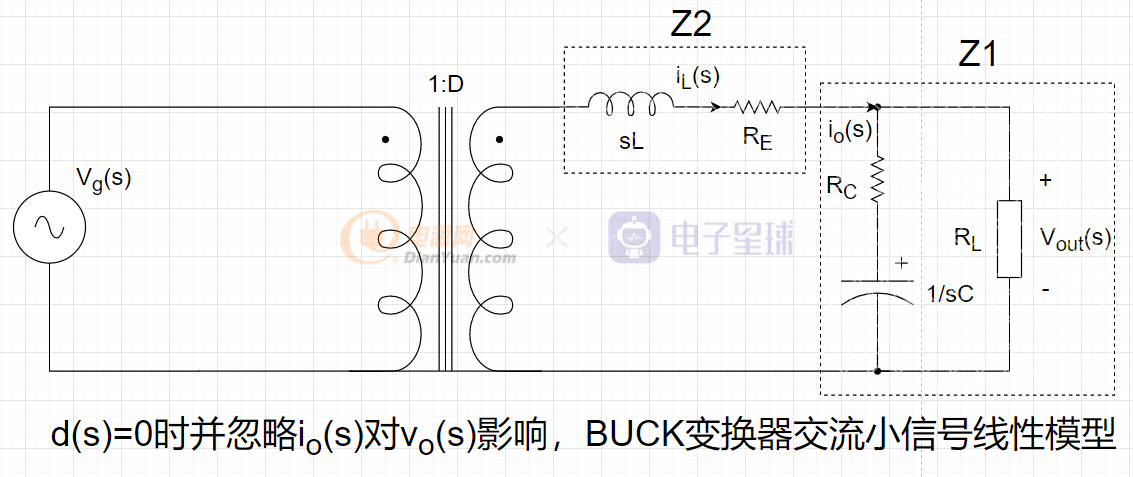
通過上圖可得:
化簡可得:
2)求Mvg傳遞函數
根據上圖中次級回路的結構,可得到方程:
化簡可得:
3)求Gpv傳遞函數
,所以要將vg(s)置零并將io(s)對Vo(s)的影響忽略,可以得到如下的框圖:
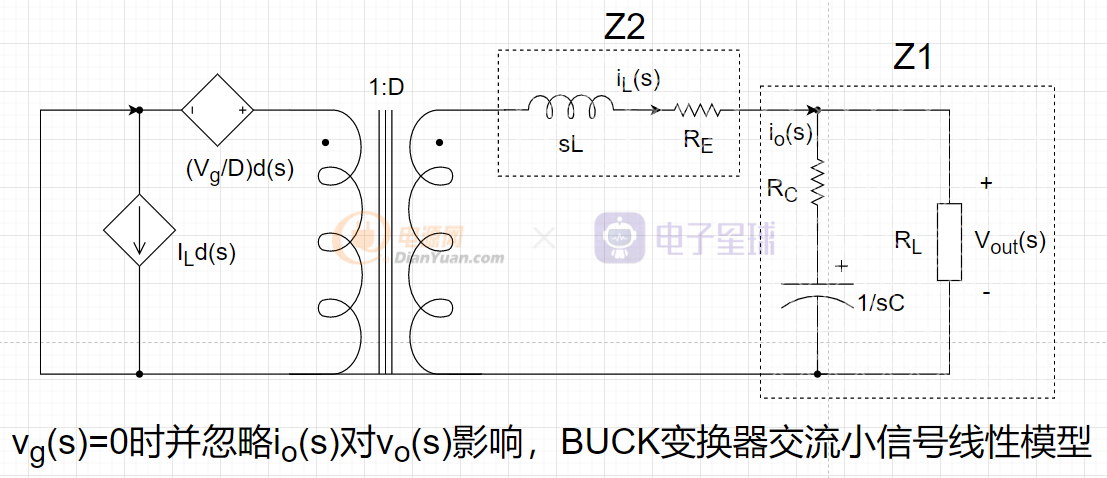
化簡可得:
4)求Gpi傳遞函數
同樣根據上圖,有如下方程:
化簡可得:
5)求Zo(輸出阻抗)傳遞函數
將vg(s)和d(s)置零,得到如下框圖:
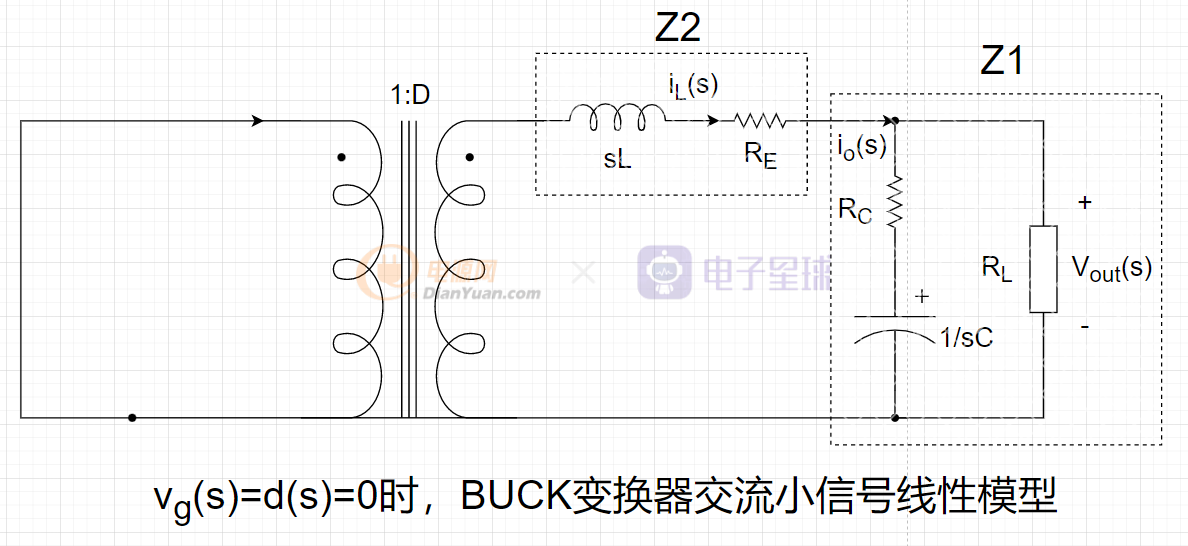
有如下的方程:
化簡:
6)求Avi傳遞函數
化簡:
至此,已經將功率級環節所有的傳遞函數推導出來。
另外,電感電流采樣環節分為兩部分:Rs(電流互感器等效電阻),He(s)(連續域電流峰值采樣傳遞函數)。
其中He(s)可以近似等效為:
式了中的,
接下來,以一個BUCK電路為例,來具體說明是如何應用上面推導出的傳遞函數計算電壓環路的補償Gvc
BUCK電路的參數如下:
輸入電壓: 30V最小 60V最大 45V額定值
輸出電壓:15V
輸出電流:10A
開關頻率:100KHz
互感器的匝比: 1:100
互感器次級取樣電阻:15Ω
電感量:28uH,等效電阻2mΩ
輸出電容:330uF,等效電阻20mΩ
一)電流內環的Bode圖:
電流內環框圖:
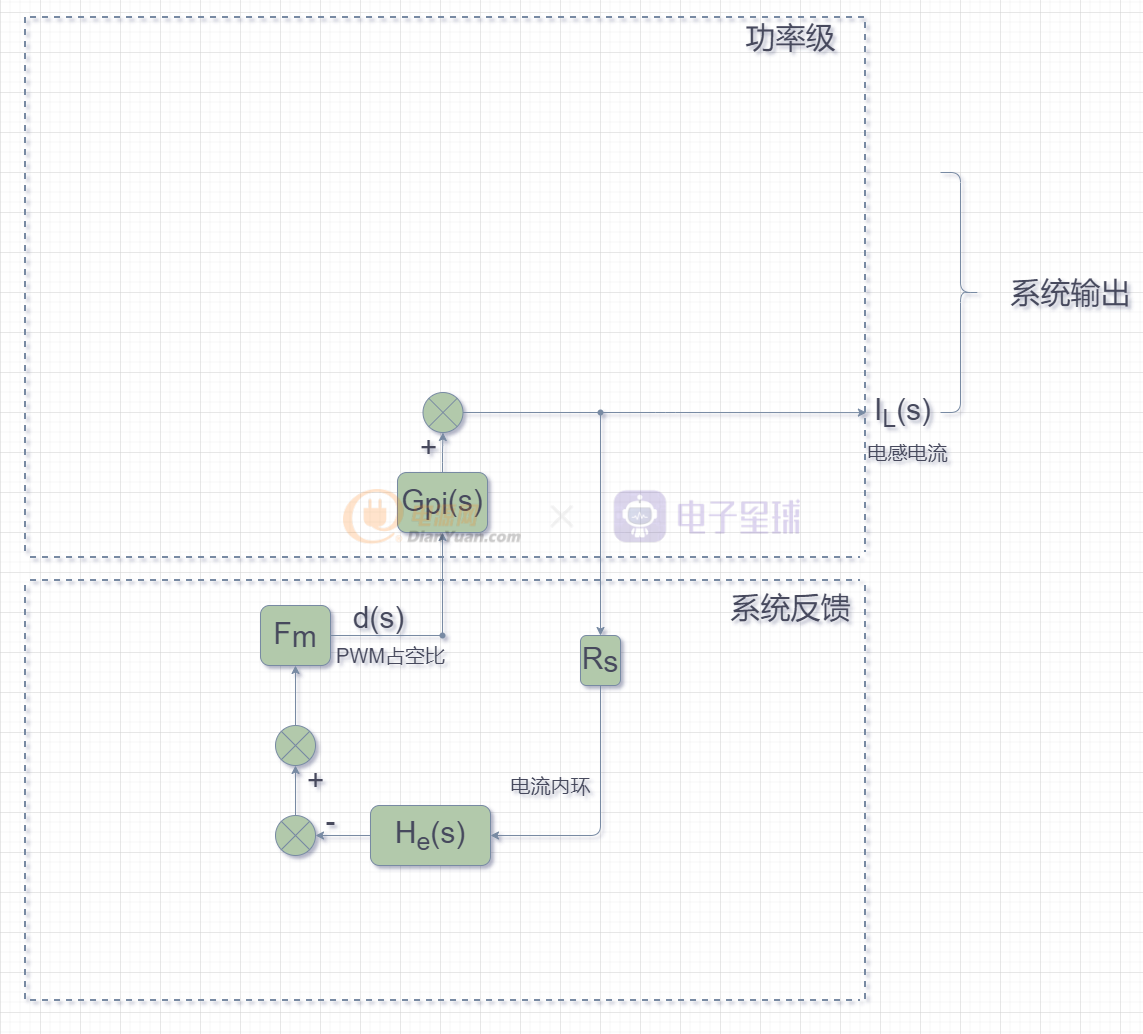
內環電流環路設計的主要目標是:找到斜率補償系數Ma的值,使電感電流IL(s)穩定,不會產生次諧波振蕩。根據上圖,可以得到電流環路的開環增益Ti(s):
其中:
用MathCAD繪制Ti(s)的bode圖,并以Ma為變量進行掃描,畫出曲線:
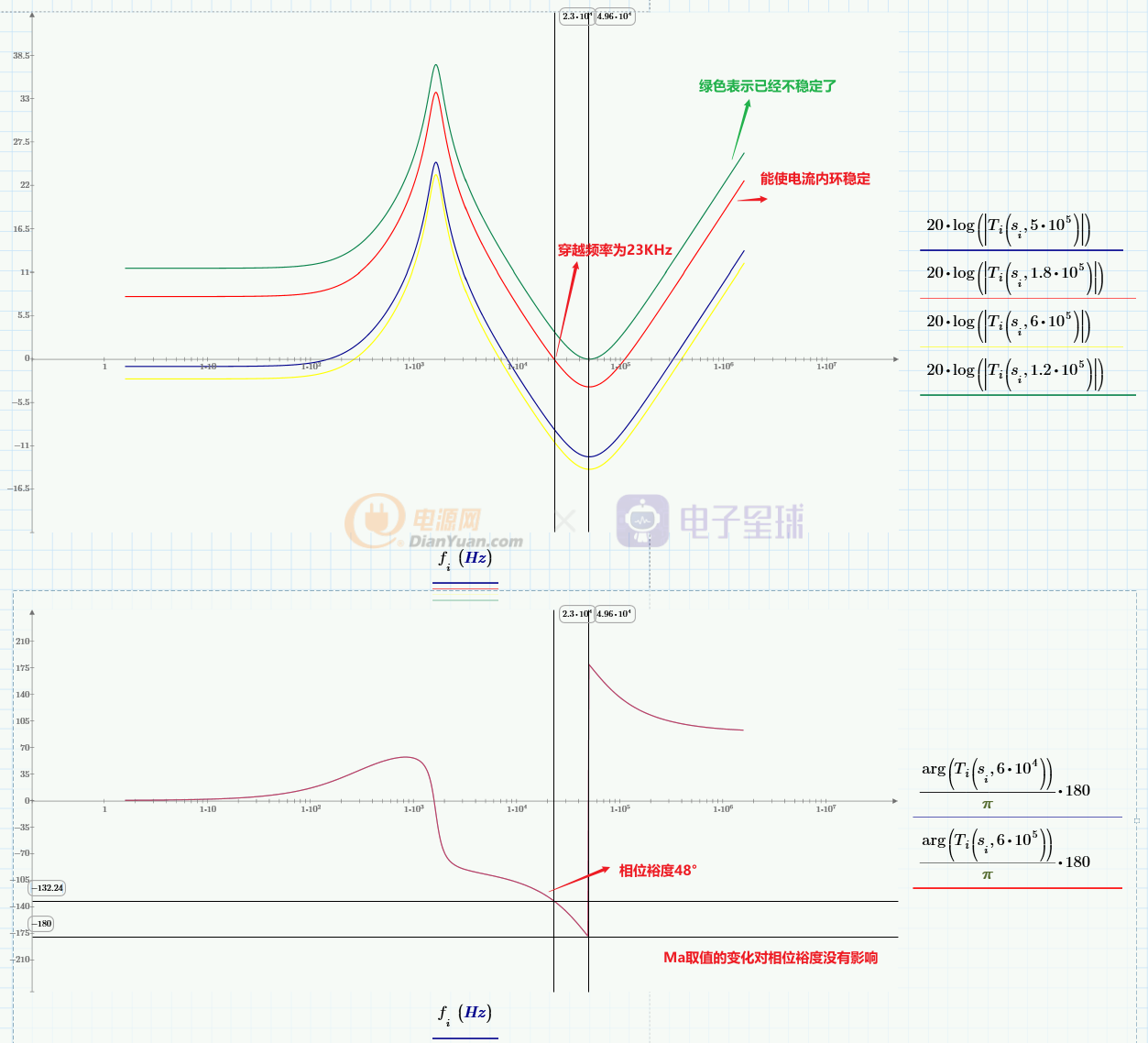
Ma的取值從1.2*10^5 A/s到6*10^5 A/s,可以得到一組曲線,當Ma小于1.2*10^5 A/sec,環路就不再穩定。Ma也不是越大越好,Ma的增大會降低穿越頻率,導致電流內環的響應變慢,還會影響抗輸入擾動的性能和輸出的阻抗。
二)控制電壓Vc(s)到輸出電壓Vo(s)的傳遞函數Ac(s):
將Vg(s)和Io(s)置零后,可以得到如下的框圖:

根據上面的框圖可以得到兩個等式:
從而可得:
畫出bode圖:


當Ma小于等于1.2*10^5以后,將會出現不穩定的狀態。隨著Ma的增大,會發現Ac(s)逐漸向電壓型控制狀態演化,當Ma取值6*10^6時,已經完全演變為電壓型控制。
在本環節,Ma的取值原則是:削掉幅頻曲線中的尖峰,同時要保證不會變為電壓型控制環路。Ma既不能太小,也不能太大。這與調試中的經驗比較吻合,Ma補償不夠時,會出現次諧波振蕩,Ma補償過大,就會變成電壓型控制。
三)抗輸入擾動Mvcl(s)(電流閉環,電壓開環情況下):
在忽略io(s)的影響且Vref置零的情況下,得到如下框圖:
根據上面框圖,可得到一組方程:
化簡:
因為要求得輸出電壓的變化,所以應當將電壓環路斷開,電流內環閉合時,畫出Mvcl的bode圖:
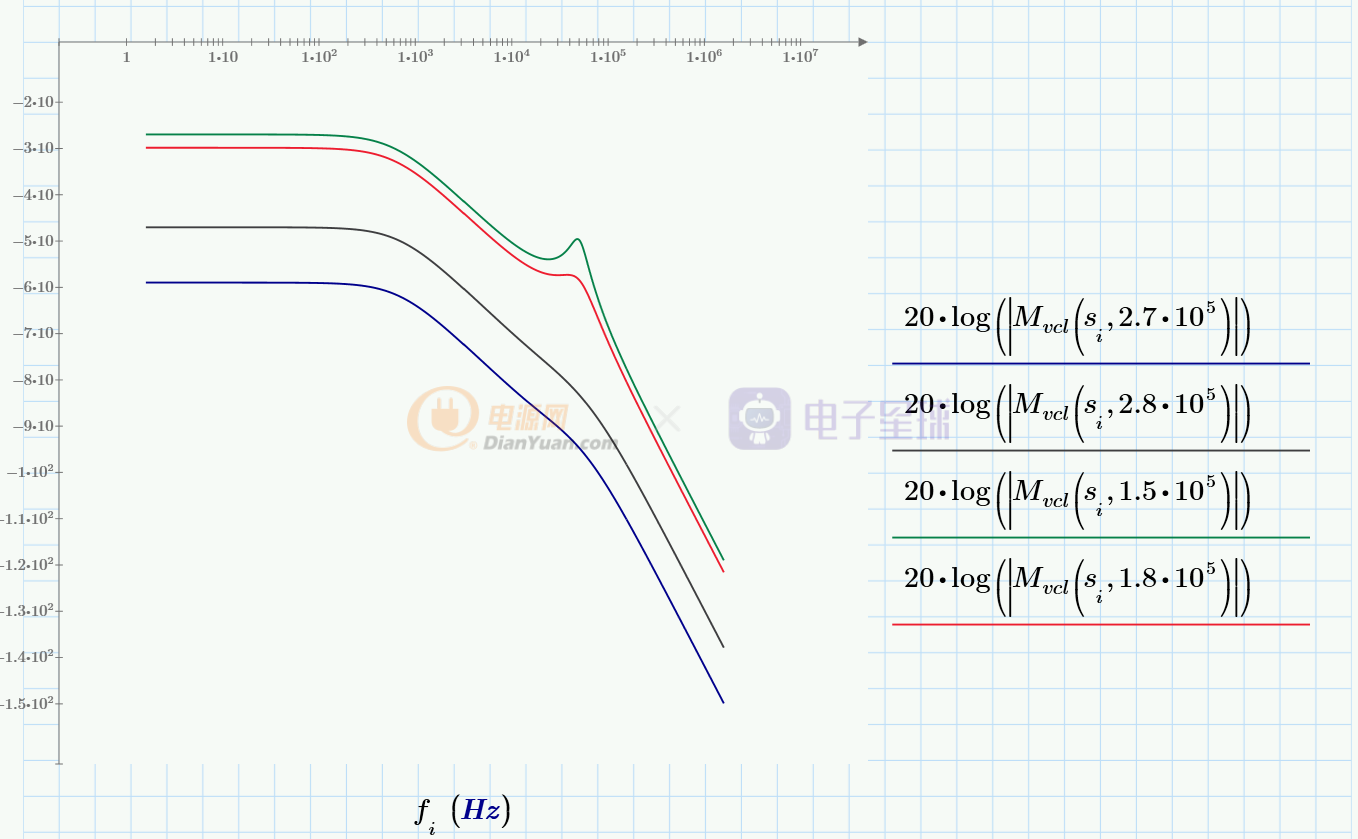
可以看到,Mvcl(s)增益越小(曲線越低),輸入電壓Vi(s)對輸出電壓Vo(s)的影響越小。隨著Ma的變化Mvcl(s)增益并不單調,當Ma取值2.7*10^5時,Mvcl的增益最低,即輸入電壓Vi(s)對輸出電壓Vo(s)的影響最小
四)輸出阻抗Zocl(s)(電流閉環,電壓開環情況下):
當Vg(s)=Vref=0時,得到如下方框圖:
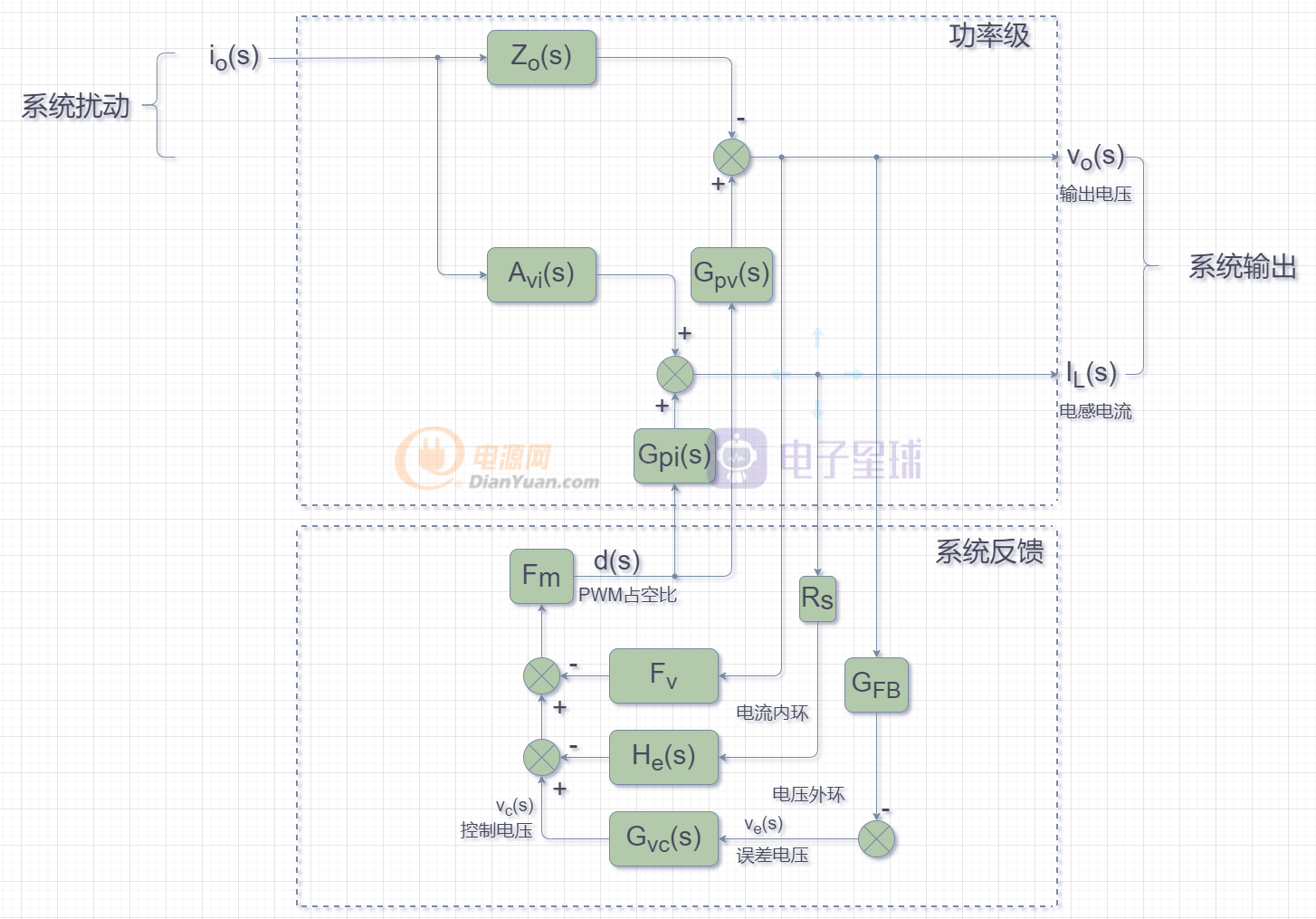
有下面一組方程:
化簡:
在電流內環閉合,電壓外環開環的情況下,畫出bode圖:
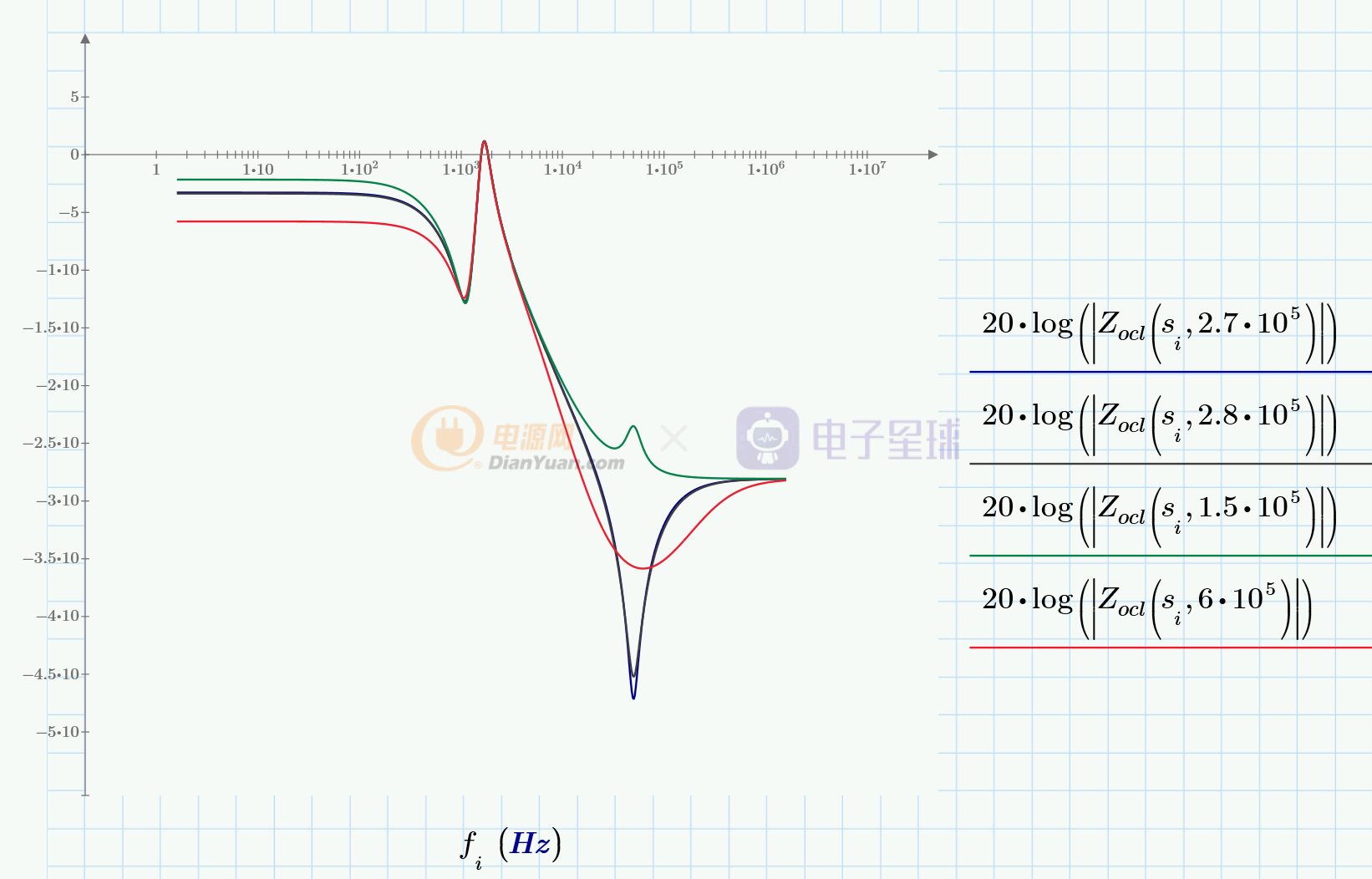
注意Zocl(s)的增益是個負數。在低頻段,|Zocl(s)|絕對值越大(曲線越低),對Vo的影響越大。即:在低頻段,隨著Ma的取值的增大(曲線越低),抵抗負載擾動的能力越差,因此從負載抗擾動的角度看,Ma的取值越小越好。
上面的計算過程,分別從電流環路穩定性、電流型向電壓型的演化過程、輸入電壓抗擾度和負載抗擾度這四個方面說明了斜率補償系數Ma的選擇原則,綜上可以選擇:
下面就以Ma這個值為基礎來計算外部電壓環路的補償參數。
首先,根據Ma的取值,畫出電流環路的開環增益Ti(s)的bode圖:
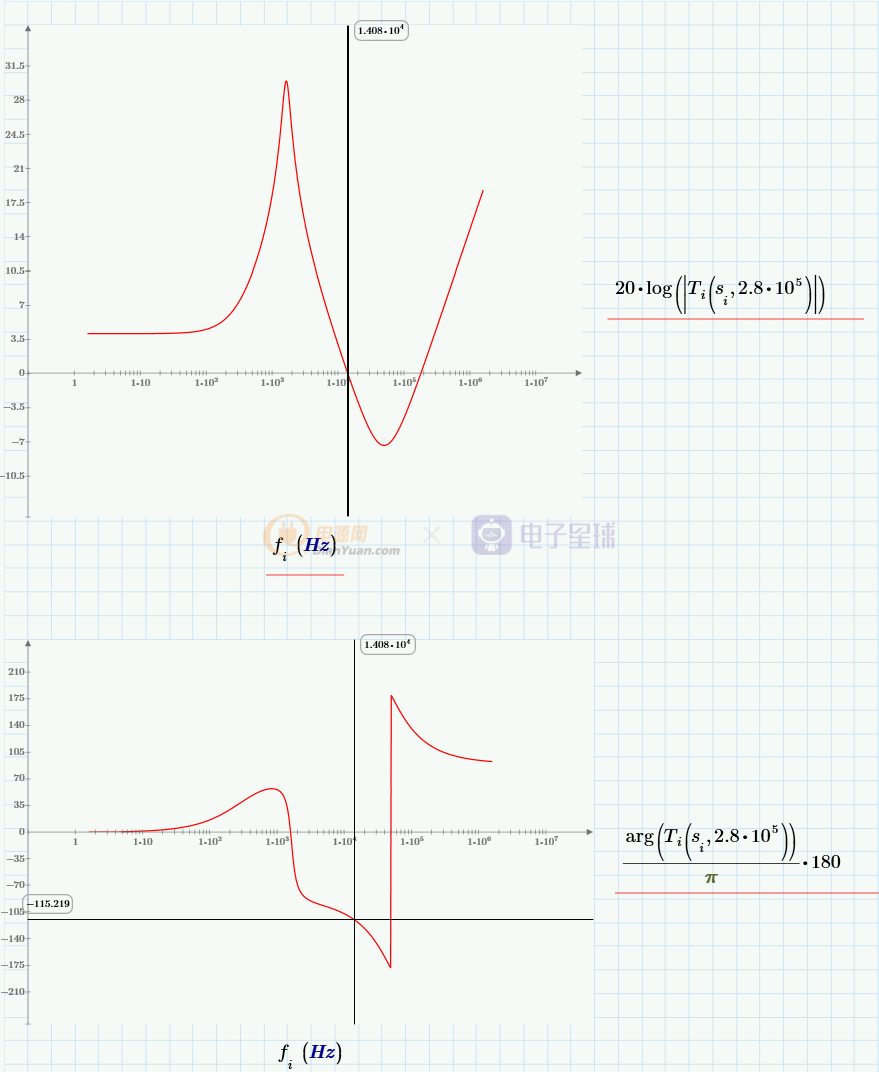
穿越頻率14KHz,相位裕度65°。
Vc到Vo的傳函Ac(s)的bode圖:
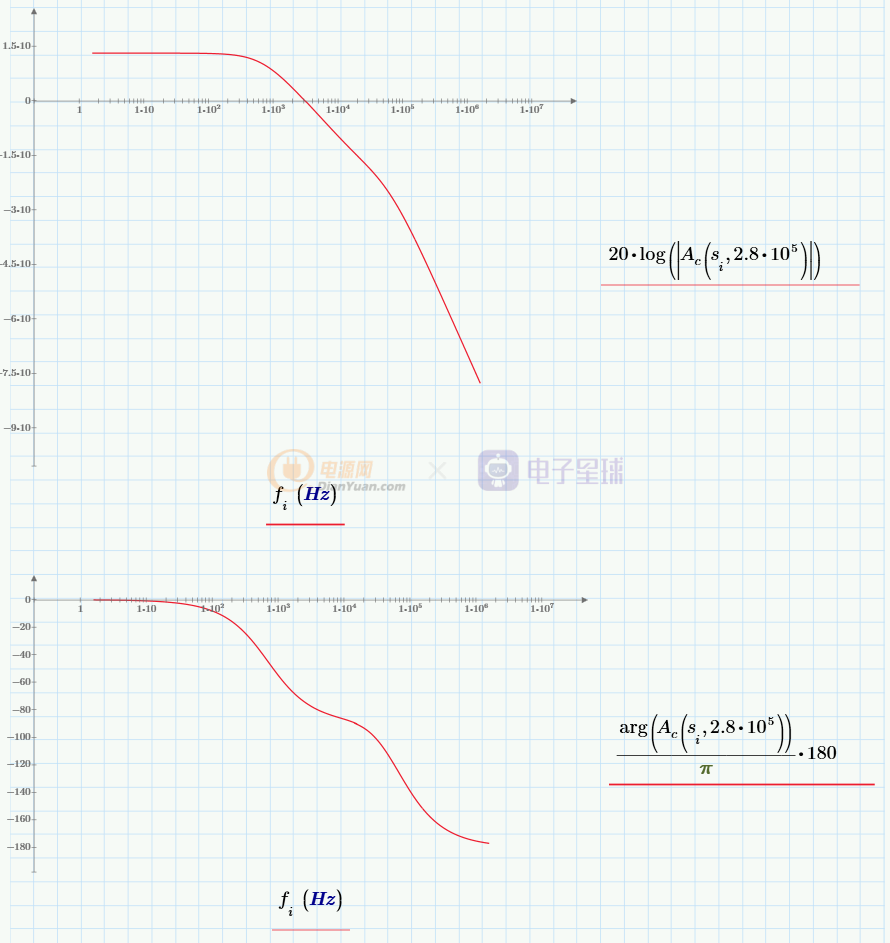
上圖中的Ac(s)已經是穩定的狀態了,只是低頻的增益比較小,穩態誤差較大。
五)電壓環路設計:
將前面的電壓環路進行整理得到框圖:
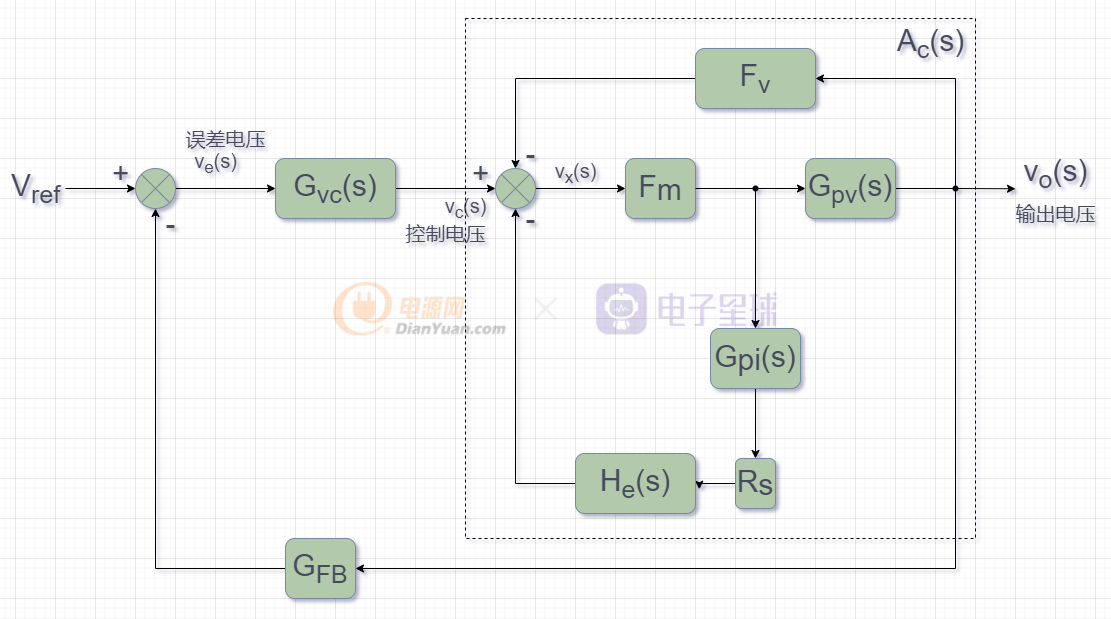
因為控制電壓Vc到Vo的傳遞函數Ac(s)已經在前面求得,所以電壓環路開環增益Tv(s)就是:
電壓環路的設計,主要是加大電壓環路低頻開環增益以消穩態誤差,并讓幅頻曲線穿越頻率盡量高些,保證快速性,因此針對Gvc(s)補償的需求,可以用下面的電路:
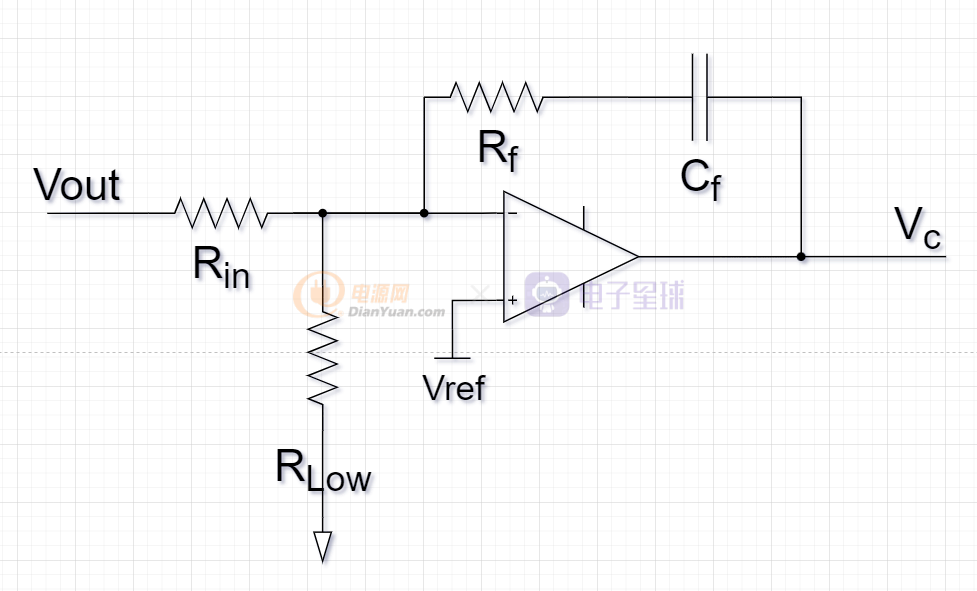
把Gvc(s)傳遞函數的零點放在600Hz,初始極點1.5KHz位置后,經過計算,得到如下參數:
Rin=10k RLow=2k Cf=10.6nF Rf=25k
根據上面參數,畫出Gvc(s)的bode圖:

需要注意的一點是:上圖中的補償器的傳遞函數已經包含GFB及相減的功能了,所以電壓環路開環增益Tv(s)改為:
然后,以上組參數為基礎,畫出Tv(s)的bode圖:
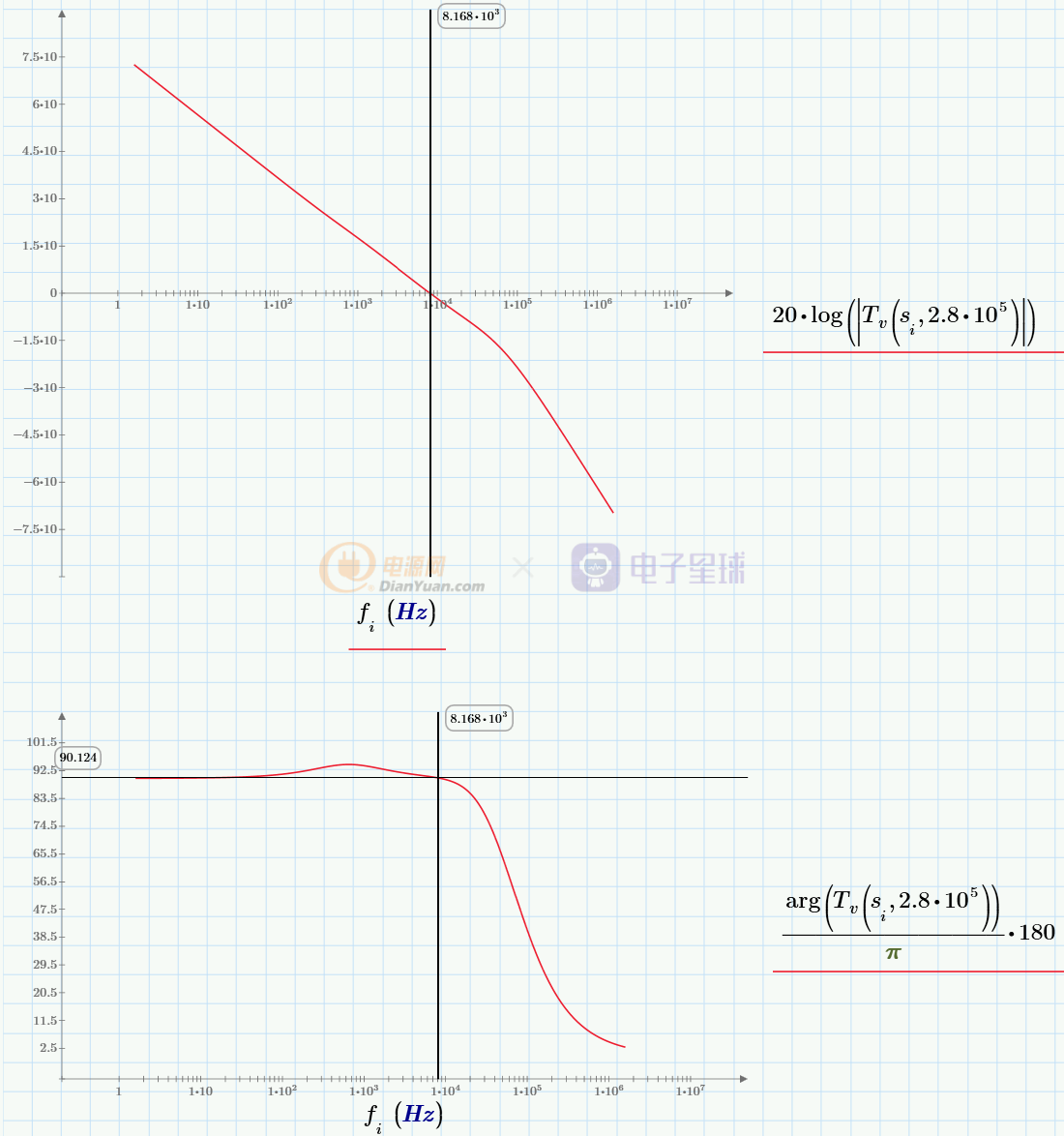
從該圖中,可以看到電壓開環bode圖的穿越頻率為8.2KHz,相位裕度為90°。
再用SIMPLIS仿真驗證上面的計算是否正確。
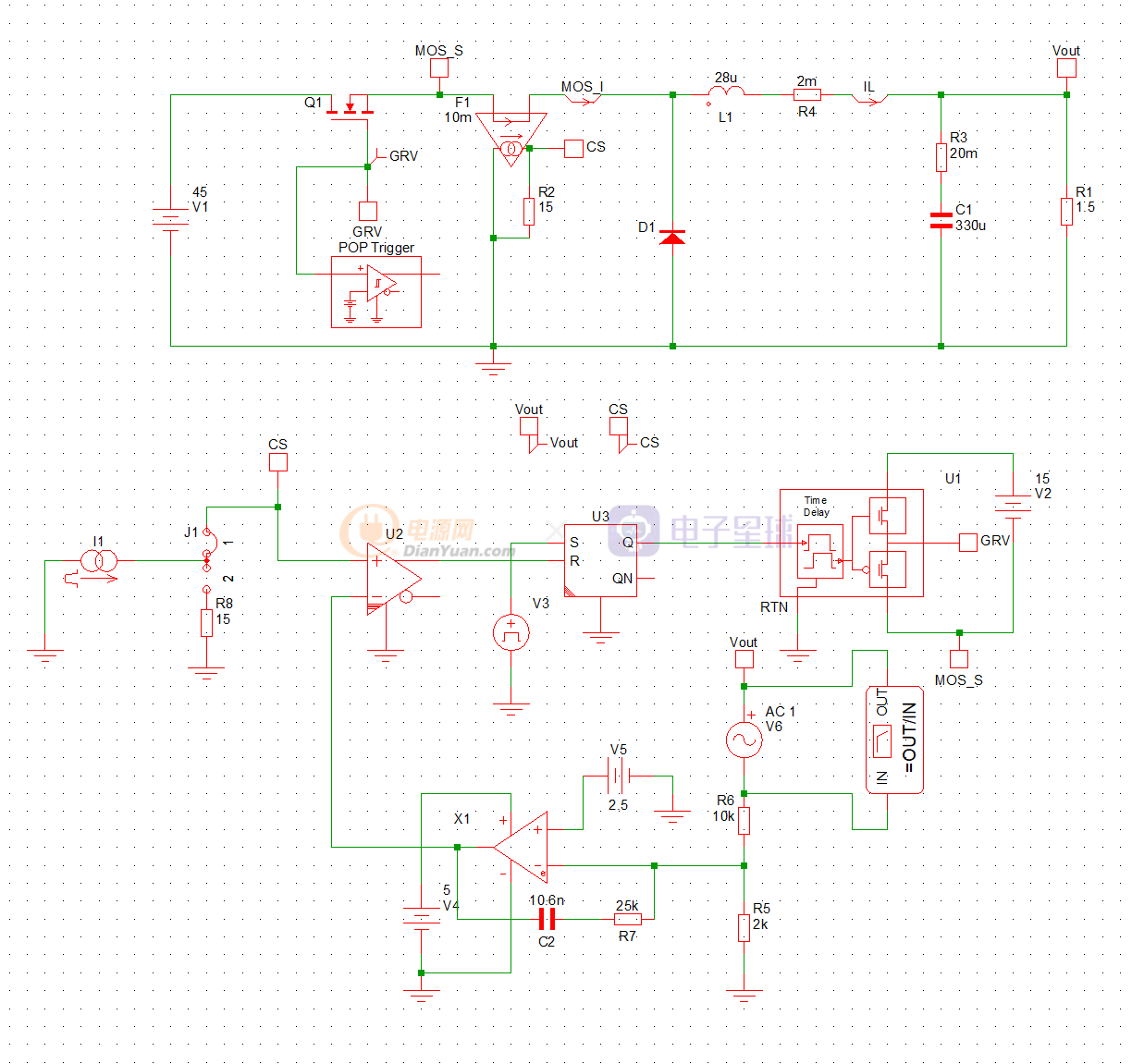
通過AC交流仿真后,得到電壓環路的bode圖:
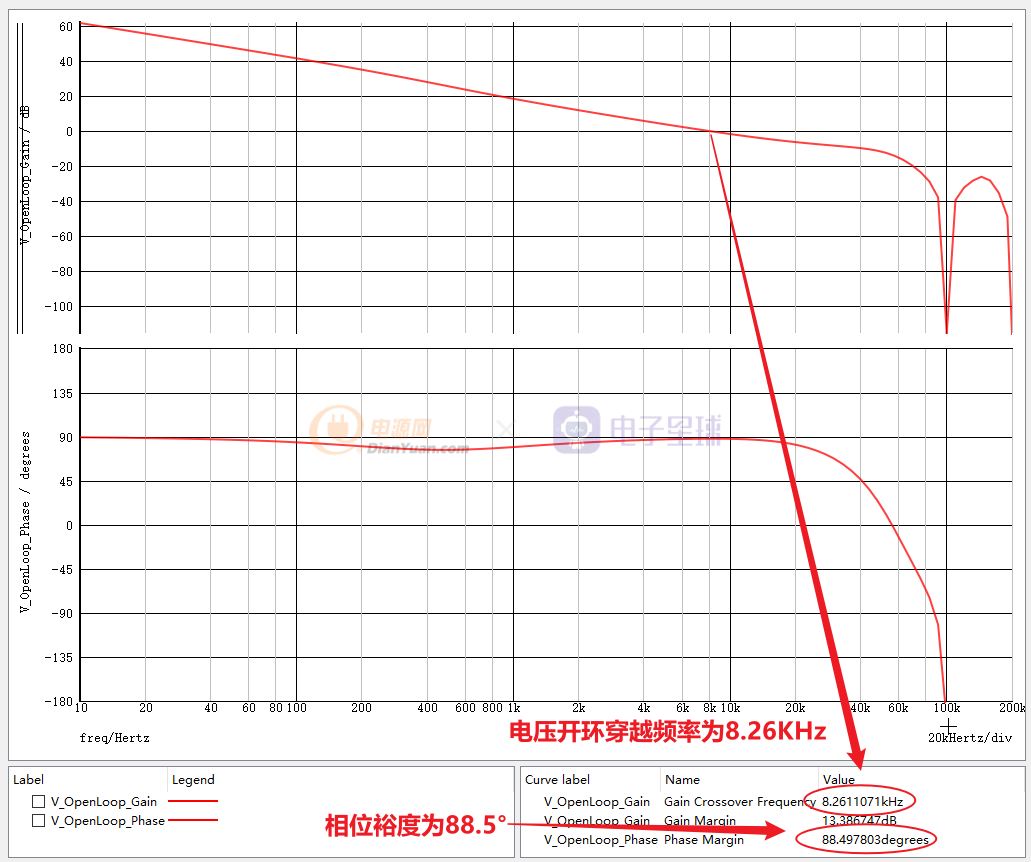
仿真得到電壓開環穿越頻率為8.26KHz,相位裕度為88.5°,與解析法計算出來的結果相一致。證明了解析法的正確性。
從仿真出來的波形看,該曲線能仿真出開關頻率對bode圖的影響,而解析法無法計算出來。
最后總結:
峰值電流控制環路計算的起點是Ma的選擇,Ma不僅影響電流內環的穩定性,還對輸入抗擾性、負載抗擾性及電壓環路也有很深的影響,通過解析的方法,可以發現Ma的變化是如何將電流型演變成電壓型的。
一般,對于BUCK電路來說,占空比不超過50%時,IL(s)是不存在振蕩的,是內在穩定的,理論上不需要斜率補償。但Ma斜率補償的選擇卻會影響電壓環路的穩定,所以即使占空比不超過50%,也應該選擇合適的Ma,然后再計算電壓補償參數。
在附件中有本例全部的計算書及仿真文件,計算書是用MathCad Prime 8.0編寫的,版本低的請自行升級。仿真文件用Simplis 8.40b版本。


