在具體分析反饋電路模型之前，我們先來簡單探討一下一個基本知識——電路的傳遞函數。

什么叫做傳遞函數呢？通俗的來說，我們把一個系統看作一個黑箱子，黑箱具有輸入和輸出，而輸出和輸入會建立某種固定的關系，這個關系可以用一個函數來表達，這個函數可以稱之為傳遞函數。舉個最簡單的例子，比如用兩個相同的電阻串聯來分壓，我們可以知道分道的電壓為輸入電壓的0.5倍，而且不管輸入電壓怎么變，0.5的比值都不變。 其實這個0.5就是最簡單的傳遞函數，整個表達式可以寫作 輸出/輸入=0.5，但是實際中我們的電路不可能永遠這么簡單，當電路更加復雜的時候，我們就需要引入另外一個概念，就是頻域。

首先我們來看一個圖上的所畫的簡單的rc電路，對于這樣一個rc電容，我們如何來計算輸入和輸出的關系呢？假設輸入是個直流信號，我們可以很簡單知道輸出是個同等大小的直流信號，那么如果輸入不是直流信號，那么輸出會是一個什么樣的信號？

雖然基本上所有的工程師都知道，這樣一個rc電路，其實就是個低通濾波器，它會衰減高頻信號，那么到底對什么樣的信號會衰減，會衰減多少，我們需要一個可以量化計算的方法，這里就需要用到頻域的概念，在頻域里面信號都是以正弦波的形式存在的，而正弦波除了有幅度，他還有頻率和相位這幾個參數，電路里面的元器件阻抗也要以負阻抗的形式存在。比如在頻域里面，電阻r還是用r來表達，但是電感l的阻抗是用 s*l來表達電容c的阻抗， s乘以1/c來表達，其中 s=ωj，ω是指的角頻率，那么這個角頻率和我們熟悉的頻率之間的關系是ω=2πf， j就是表示的復數。

這樣一來我們可以知道，除了電阻，電感和電容的阻抗會隨著頻率變化，電感的阻抗會隨著頻率的增大而增大，而電容則相反。得到了這些元器件的復阻抗表達式之后，我們就可以利用基爾霍夫定理在頻域里面計算出簡單的rc電路的傳遞函數，那么我們得到這樣一個傳遞函數 輸出/輸入=1/（scr+1）。

其實這里的話就是一個以復數形式表達的傳遞函數，而對于復數來說，它是可以求模，那么膜在實際意義里面其實就是信號的增益，也就是輸出信號的有效值和輸入信號之間的比值是放大了還是縮小了？放大倍數又是多少？可以用增益來表達。那么復數還可以求角度，也就是我們實際情況意義里面的像，也就是輸出的信號的相位減去輸入信號的相位得到的相位差。總而言之，復數形式表達了傳遞函數，既可以準確反映信號幅度的變化，也可以反映信號相位的變化。

那么在這里要注意的是 s這個符號，剛才講過s=ωj那么其中包含了一個變量，ω就是角頻率，也就是說當信號的頻率變化的時候，s就是個變量，這個變量會導致傳遞函數的模和角度會隨著頻率的變化而變化。如果我們把幅值和頻率的關系圖描繪出來，就可以得到個增益曲線，把相位和頻率的關系圖描繪出來，可以得到一個相位曲線，那么這幾個曲線我們稱之為波特圖。

在這里我們留個思考題，假如說我們有一個兩級rc濾波器，那么這個濾波器的傳遞函函數會是怎么樣的？大家可以去推導一下。

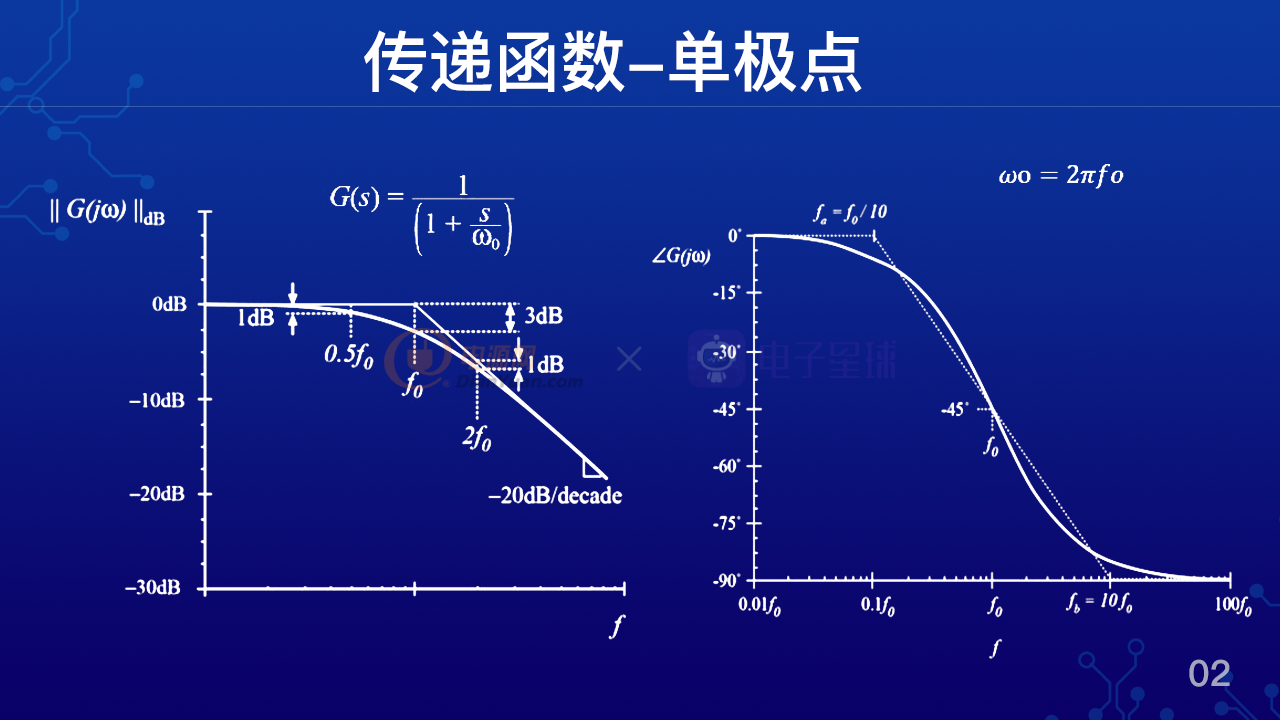
在剛才我們已經求出了rc濾波器的傳遞函數，但是這樣的傳遞函數表達了什么樣的物理意義？如果單從公式來看很難理解，但是如果我們把這個函數求模，求出來的模再做對數運算，再乘以20，也就是說把它轉化成分貝，那么在以頻率為橫坐標，分貝為縱坐標就可以得到一個增益的波特圖，也就是左邊這個曲線。

那么我們看曲線可以得知增益會隨著頻率的增加逐漸降低，并且在f0這個頻率點降低了三個db，那么我們稱之為 f0頻率點為轉折頻率點。最后的話我們可以看到爭議會議20db10倍頻的斜率下降，對于這樣特性的函數，我們稱之為單極點特性，極點的位置就是轉折頻率點，就是我們剛才所說的f0。

那么如何計算這個f0的值，我們可以先把傳遞函數寫成標準模式，就是我們圖上所示的G（s）=1/（1+s/ω0），那么其中ω0就是極點的位置。如果我們把剛才rt濾波器的傳遞函數也寫成這樣的標準模式，那么就可以寫成 Vout/Vin= 1÷（1+ s）÷1/rc，那么這里也可以得到ω0=1/rc，那么轉化成f0，就是f0=2π 1/rc，也就是說其實rc濾波器表現出來就是單極點特性，而這個極點的位置在2π 1/rc。

對于增益圖，通常為了簡化分析，理論上可以用漸進性，也就是圖中的折線來代替，折線的轉折點就是轉折頻率點，采用折線來近似，非常適合早期沒有計算機的時代，可以大大簡化波特圖的分析和理解。但是現在計算機如此的發達，我還是建議大家利用計算機來匯出完整的增益曲線。

同時我們知道復數表達的函數，還有相位角度的問題，那么右圖就是單極點傳遞函數的相位曲線。

我們可以看到在轉折頻率點相位之后正好45度，但是相位其實從遠遠小于轉折頻率的地方就開始滯后了，一直到無窮大頻率處，最后總共滯后90度。換個說法，就是一個單極點會帶來90度的相位之后，那么如果為了簡化分析，我們也可以做一個近似，通常就認為在1/10轉折頻率點，相位就開始滯后，到轉折頻率點，正好滯后45度，再到10倍的轉折頻率點，認為它已經滯后了90度。就這樣我們把具有單極點特性的傳遞函數的波特圖描繪了出來。

從增益曲線上我們可以看到，增益在頻率接近0的地方為0db，也就是一這意味著在低頻段輸出接近輸入，但是隨著頻率的增加，增益開始下降，呈現出明顯小于一的特性，這就意味著信號被衰竭了，驗證了低通濾波器的特性。那么從相位曲線也可以看到，在低頻段相位滯后很少，但隨著頻率的增加，最終會滯后90度。那么這個就是整個低通濾波器表現出來的特性，我們也可以稱之為單指點特性。

除了表現為單極點特性的傳遞函數之外，我們再來看一下其他類型的傳遞函數工。比方說我們把這個單極點的傳遞函數做一個倒數運算，就可以得到這樣一個表達式，就是G（s）=（1+s/ω0） 。如果我們把這個表達是求膜求相位，就可以把波特圖描繪出來。

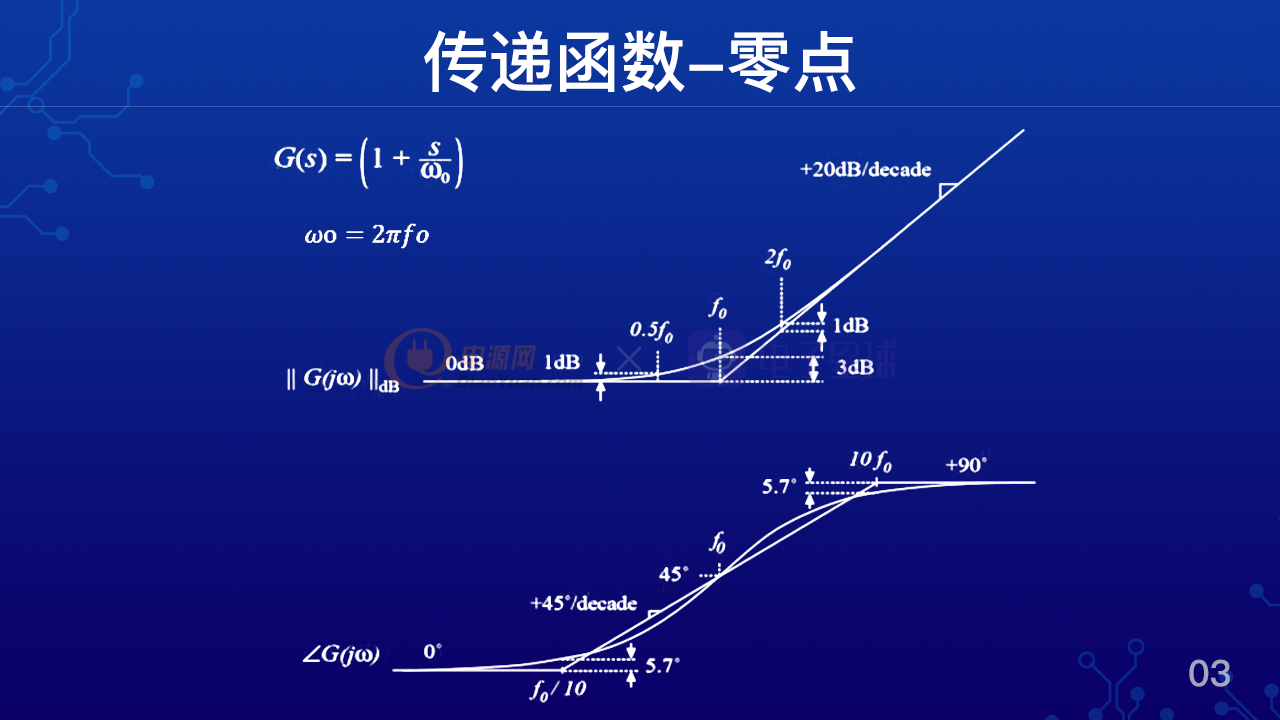
可以看到如圖所示的兩個曲線。我們先看上面的增益曲線，從這個增益曲線可以看到增益從0db 開始，然后到接近f 0的地方開始上升，到f 0處上升了3個db，最后他會以20db每十倍頻的斜率上升。我們馬上就會意識到這個增益曲線其實和極點正好相反，那么我們稱之為零點，這個零點的位置就是f 0，如果以角頻率點表達，就是ω0。那么再看下面的相位曲線呢，可以近似的認為從十分之一的轉折頻率開始超前，在零點的位置超前45度，到10倍轉折頻率處超前90度。

所以說零點的特性和極點是完全相反的。這就是我們為什么會經常聽到說用一個零點去補償一個極點的說法。因為他們兩個是對偶的是互補的，是可以互相抵消的。

除了極點和零點，那么我們再來看另外一個表達式，G（s）=1-s/ω0 。那么和剛才那個零點的表達是不同的是，0點是1+s/ω0，這里是-s/ω0。

這個表達式呢就是表示了一個右半平面0點。這個右半平面零點在波特圖中的表現形式為增益隨著頻率上升，但是相位卻是隨著頻率滯后。也就是說它的增益曲線和零點相同，但是相位曲線卻和極點相同。

那么在什么樣的系統里會碰到右半平面零點呢，就在ccm 模式的boost ，或者Buck/Boost或者反激這些拓撲中會碰到這個右半平面0點。

那么右半平面零點在電源系統中具體表現是什么呢？比如在boost 中，如果負載突然變重，輸出電壓下跌環路會加大占空比。但這個時候整流管的的占空比一減力就會相應變小。

但此時電感電流卻沒有立即升起來，會導致不適的整流管輸出平均電流反而減小，從而進一步加劇輸出電壓下跌。這就是右半平面零點的物理特性。理論上來說，右半平面0點可以用右半平面極點來補償。

但是事實上在我們的開關電源系統中，我們沒有辦法在補償電路中構建這樣一個右半平面極點。所以這個右半平面零點我們根本沒有辦法補償。這也就意味著具有右半平面零點的拓撲在環路上具有嚴重的局限性。

在了解了一些基礎傳遞函數的增益特性和相位特性之后，我們來看一下，如果把這些基礎函數乘起來，就可以得到更加復雜的傳遞函數。

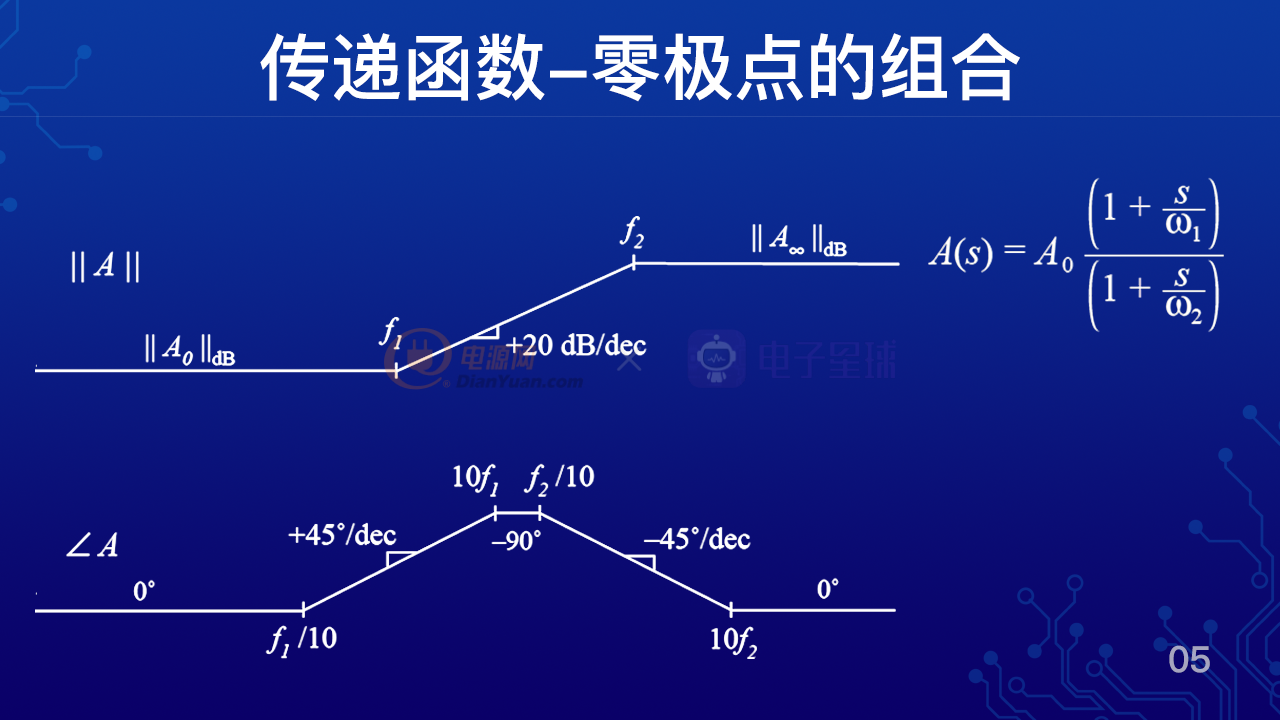
如圖所示，我們可以把一個極點和一個零點的傳遞函數相乘，可以得到這么一個表達式。

A（s）=A0*（1+s/ω1）÷（1+s/ω2），這個表達式里面包含了一個極點和一個零點，A0是直流增益，ω1為一個零點，ω2為一個極點。

如果ω1=ω2，我們可以得到這個函數會變成極其簡單的比例函數，就是A（s）=A0。這種函數的增益曲線和相位曲線都會變成一條直線，也就是我們常說的零極點互相補償，互相抵消。

那么如果ω1≠ω2，假如ω1<ω2，我們就可以得到如圖所示的波特圖。

首先看上面的增益曲線，我們可以發現隨著頻率的增加，我們先碰到一個零點，ω1或者f1過了零點之后，爭議以20db每10倍頻的斜率上升，等到了ω2或者f2這個頻率點，我們又碰到了一個極點，增益就不再上升，后面的增益曲線就變平了。

那么再看一下下面的相位曲線，相位在十分之一ω1處開始超前，到10倍的ω1處超前了90度，在十分之一ω2處開始滯后，最終在10倍ω2處滯后的90度，這樣一個超前一個滯后，他們互相抵消就可以得到高頻處的相位和低頻處的相位是相同的。也就是說最后總共的相位超前或者滯后只有0度。

但是在這里我們要注意一下，這里有個前提假設，假設10倍的ω1要比十分之一的ω2還要小，如果10倍的ω1是要大于十分之一的ω2，我們就會發現中間拱起來的相位超前不會達到90度，因為它還沒有達到90度，就會被ω2這個極點影響，從而轉向開始下降。

所以大家可以想象一下，這種情況下，如果ω1和ω2開始靠近，增益曲線和相位曲線又會怎么變化呢？那么再當ω2小于ω1的時候又會怎么樣？大家可以去思考一下。

除了上述所講的單極點、單零點以及零極點的組合之外，在開關電源系統里面，我們還會碰到更加復雜的傳遞函數，那就是復合雙極點。比如常見的lc濾波器的傳遞函數，就是一個典型的復合雙極點。復合雙極點和單純的兩個極點相乘不同，復合雙極點有時候是無法解析出三個節點來的，我們不能簡單的把它認為是兩個極點的組合，必須統一起來分析。

復合雙極點標準表達式為：

其中ω0為轉折頻率，Q為品質因素，簡單的來講，雙極點的增益曲線表現為過了轉折頻率之后，以40db每10倍頻的斜率下降，這種斜率是單極點的兩倍。

但是復合雙極點還有一個特性，那就是Q值。當Q值很大的時候，就是左圖最上面的曲線，表現為在轉折頻率點增益會變得很大。那么隨著Q值的降低，轉折頻率點的增益也逐漸降低，越往下面的曲線表現為Q值逐漸降低。 右邊是相位曲線，我們可以看到當Q值大的時候，相位之后的非常快，如同跳水一樣，在很窄的頻率范圍內就可以實現180度的相位滯后，但是Q值低的時候緩和很多。

那么符合雙擊點到底能不能解析為兩個單極點的組合？其實當Q小于等于0.5的時候，我們可以把復合雙極點解析為兩個單極點的組合。比方說當Q=0.5的時候，我們可以把復合雙極點解析為兩個單極點，這個時候兩個單極點在同一個位置，就是ω0。事實上這種復合雙極點在我們開關電源系統里面是很常見的。

剛才我們講到復合雙極點是個比較復雜的表現形式，但是我們知道當Q小于等于零0.5的時候，可以解析為兩個單極點組合。

剛才已經講了，Q=0.5的時候，可以解救一對位置相同的極點。那么Q<0.5呢，在早期計算機不是很發達的時候，為了簡化理解，我們通常會做一些近似，那就是當Q明顯小于0.5的時候，可以把這對復合雙極點分解為兩個單極點，一個為Q乘以ω0，另外一個有1/Q乘以ω0，這樣就很容易理解和計算。

當然實際上現在隨著計算機技術的發展，我們已經很少在應用的時候采用手動記賬，而是采用計算機軟件進行計算，比如Mathcad的excel等工具就可以。所以這種近似的方法已經不是那么重要了。但是對于學習的人來講，還是有一定的意義。