經(jīng)過我一周的學(xué)習(xí)和研究和2夜失眠,終于搞明白信號與系統(tǒng)中的零極點及拉普拉斯變換。其實沒有想象中的復(fù)雜。學(xué)習(xí)的時候我是帶著問題學(xué)習(xí)的,就是解決開關(guān)電源設(shè)計中,為了負(fù)反饋的穩(wěn)定所加的補償電容電阻是怎么計算的,為什么這樣算的問題。
國內(nèi)很多教材和資料講的太高大上,學(xué)完了還是稀里糊涂的。本貼就是解決這個問題的。

經(jīng)過我一周的學(xué)習(xí)和研究和2夜失眠,終于搞明白信號與系統(tǒng)中的零極點及拉普拉斯變換。其實沒有想象中的復(fù)雜。學(xué)習(xí)的時候我是帶著問題學(xué)習(xí)的,就是解決開關(guān)電源設(shè)計中,為了負(fù)反饋的穩(wěn)定所加的補償電容電阻是怎么計算的,為什么這樣算的問題。
國內(nèi)很多教材和資料講的太高大上,學(xué)完了還是稀里糊涂的。本貼就是解決這個問題的。
第一章:極坐標(biāo)與歐拉公式
一、極坐標(biāo)
對于一個點的坐標(biāo),我們常用直角坐標(biāo)系來表示。這也是我們最最常用的方式。如圖1.1所示:
圖1.1
對于圖中的A點相當(dāng)于向東走4步,再向北走3步即可到達。
然而還有一個坐標(biāo)系表示法,那就是極坐標(biāo)。相同的A點用極坐標(biāo)表示如圖1.2所示。
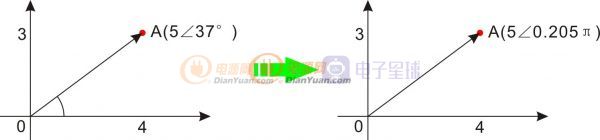
圖1.2
對于圖中的A點,相當(dāng)于逆時針旋轉(zhuǎn)37度后再走5步。然而角度的單位是度,不是數(shù)字1,對于運算來說很不方便,所以我們用弧度表示角度。你還記得嗎,360度對應(yīng)的弧度是2π。
直角坐標(biāo)系和極坐標(biāo)系雖然都能表示同一個點,但他們代表不同的模型。比如汽車的運動用直角坐標(biāo)系,輪胎的運動用極坐標(biāo)系。
對我們電子專業(yè)的人來說,發(fā)電機就是旋轉(zhuǎn)的,所以我們用極坐標(biāo)系來描述建模信號系統(tǒng)是最合適的。
二、歐拉公式
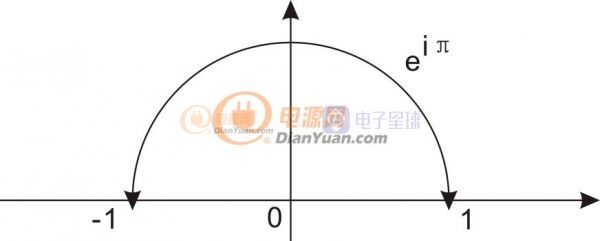
極坐標(biāo)是圖形,用什么公式表達呢?答案就是歐拉公式。
用圖形表示就是1旋轉(zhuǎn)了π度。好了,這下我們知道,以e為底的iθ就是旋轉(zhuǎn)θ度。e的i2π就是轉(zhuǎn)動一圈。
三、發(fā)電機的建模
我國發(fā)電機是50Hz/220V交流電,換句話說就是1秒轉(zhuǎn)50圈,一圈是2π,所以這個發(fā)電機用公式表示就是e^i2π50t。通用公式就是e^i2πft。
2πf就是我們常說的角頻率,通常用ω(歐米伽)表示。所以上述模型可以寫成e^iωt。
又因為字母i在電路中已經(jīng)表示電流了,所以電路中我們用j代替。兩個字母是一個意思,所以上述模型又可以寫成e^jωt。
四、發(fā)電機在復(fù)數(shù)中的表示
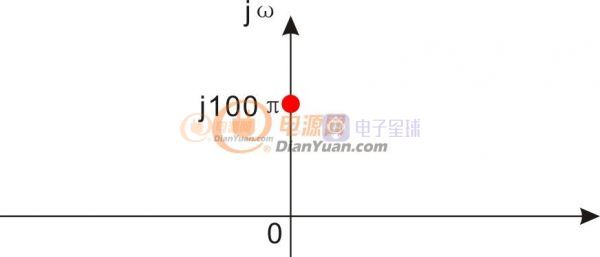
jω我們單獨抽出來,用復(fù)數(shù)或者用復(fù)平面表示,看看應(yīng)該是什么樣子的,答案是下圖中紅點位置。這個紅點就表示了這個發(fā)電機轉(zhuǎn)速特性。
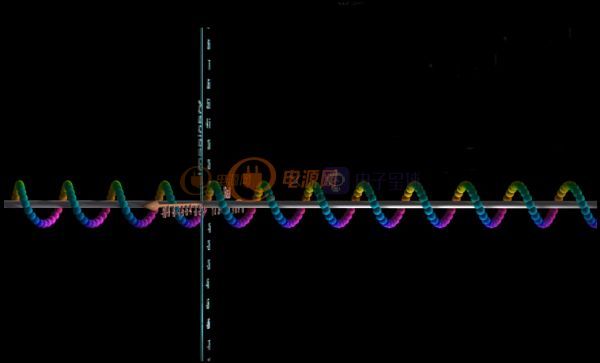
借用國外的一張視頻圖就是下圖這個樣子的波形,等幅旋轉(zhuǎn)。
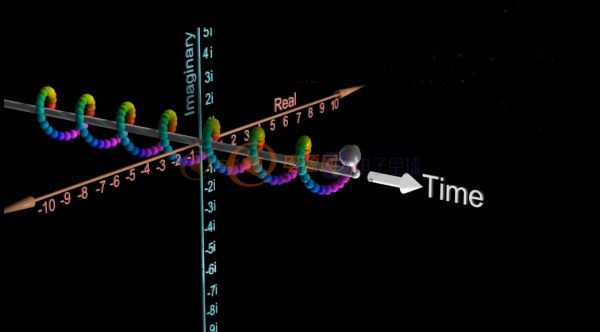
從側(cè)面看就是我們熟悉的正弦波,等幅振蕩。
好了,今天先寫這么多吧,我表達清楚了嗎?