聲明：

本文是業余時間的思考成果展示，其中可能有不太正確的地方，歡迎指出！另外不注明原作者的轉載都木有小JJ！

背景簡介：

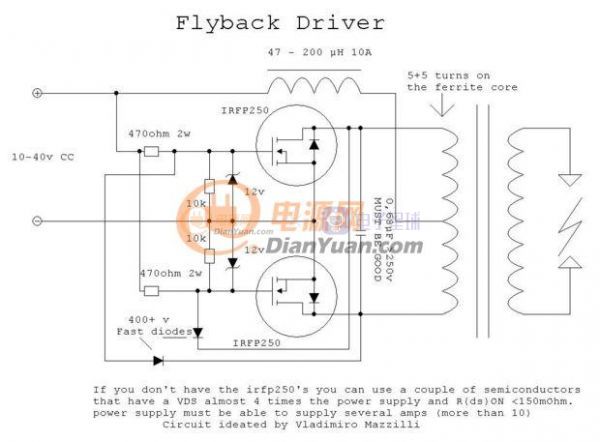
ZVS雙管自激電路（以下所有ZVS均指這個電路而不是零電壓開關除非特別說明），基本上每一個在論壇上玩高壓或者電路的同學都做過或者至少聽說過的一個電路。如下圖：

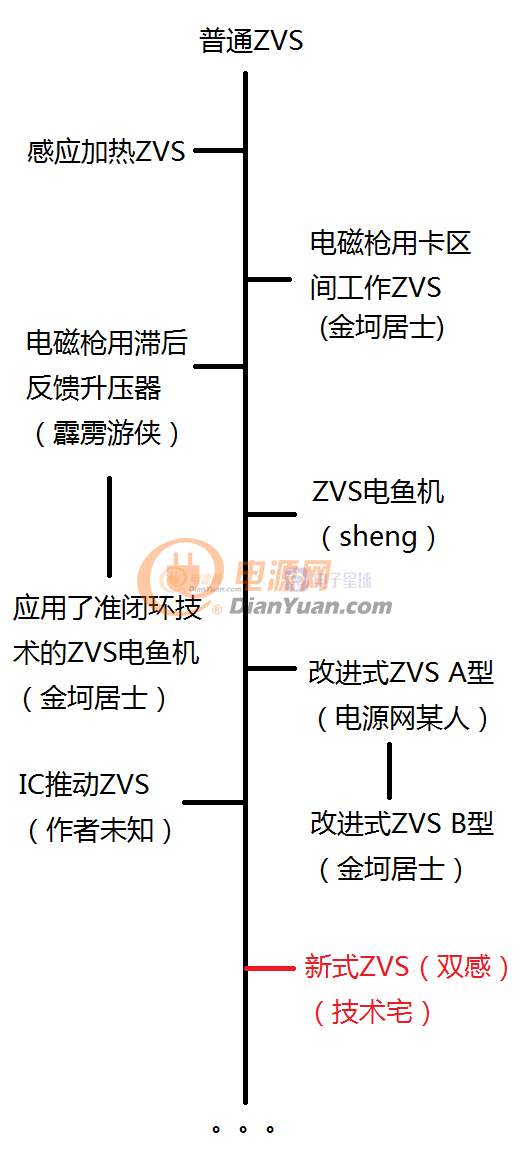
還有隔壁科創論壇的yanli12321同學發明的雙電感的無抽頭變壓器版本，這里就不貼圖了，空降地址就是前面的鏈接。在中二時期，窩還嘗試過給ZVS加上穩壓電路，有滯回比較器法還有間歇使能的準閉環（帶空載輸出過壓保護的ZVS電魚機和第一次準閉環ZVS的想法），在缺少理論論證的情況下進行的設計，效果并不是很細想，很多現象無法解釋，某些蜜汁故障無法確定原因無法排除。還有一個當年的黑粒屎教程...盡管如此，ZVS還是給論壇各位包括窩的學生時代留下了十分美好的回憶，下面是中二時代的ZVS發展歷史:

雖然被制作過了無數遍，但是這個電路的工作原理確從來沒有一個詳細的解釋，唯一的分析就是科創論壇上面的這篇文章，但是他也沒有一個詳細定量的分析。這就是這片文章存在的意義！有史以來第一次定量分析ZVS的工作原理并為元器件的選擇和工作點的設置提供指南。而且窩經過分析和仿真得出一個震驚的結論，ZVS里面兩個MOS會有一定共通時間，而且這個共通時間對于正常工作來說是很關鍵的。好奇為啥？那就繼續往下看吧。

在閱讀了以色列Ben-Gurion University of the Negev大學Daniel Edry的一片IEEE學報(Capacitive-Loaded Push-Pull Parallel-Resonant Converter, 會議和期刊版)之后，結合仿真，窩提出了一組適用于分析zvs的方法。注意，這個帖子給出的方法只適合于全波/全橋整流濾波型負載的ZVS，而阻性或者弱感性負載（比如感應加熱，非整流濾波的高壓電弧）不在本貼討論范圍之內，帶整流容性負載和阻性負載的時候，ZVS的特性是不一樣的，這個值得注意。窩會在另一篇帖子里給補全的，本帖只分析整流濾波負載的ZVS。

繼續Edry前輩的故事：

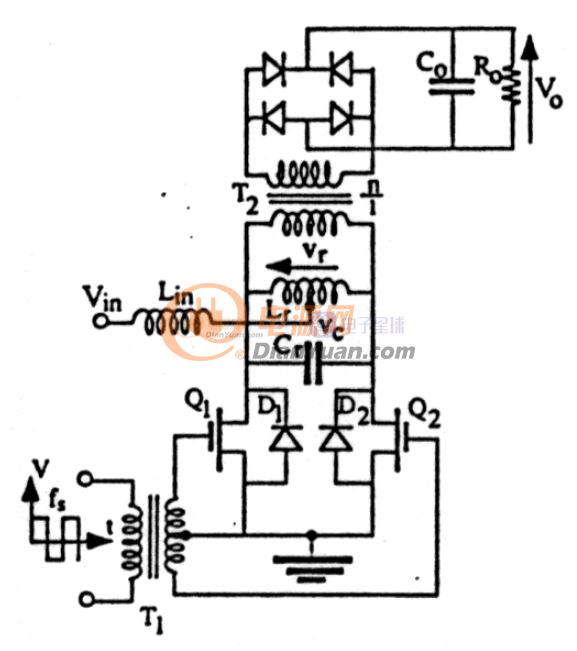
在Edry的文章里介紹了一種它激變頻固定占空比的電流源供電的并聯諧振變換器(Current-Fed Parallel Resonant Converter)，如下圖：

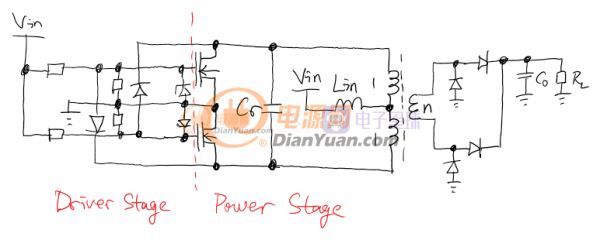
光看功率級部分完全是和ZVS一一對應的！ 窩的分析方法絕大部分地方借鑒了Edry的思路，窩稍微改進了下，使得分析時所有的量都是實實在在的可以測到的物理量，Edry的模型里有些量并沒有實際對應的物理量，雖然沒錯但是好不方便實踐測量...被分析的ZVS電路如下：

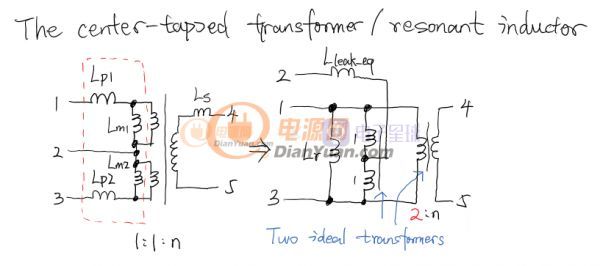
在分析的時候先只看功率級也就是Power Stage。為了分析功率級特性，先把自激部分去掉，改用外部固定頻率進行驅動。首先是處理變壓器(匝數比1:1:n)抽頭的問題，變壓器初級是一個有抽頭的電感器，在同一磁芯上同向繞制的兩個的線圈的總電感量是兩個電感量與2倍他們之間互感之和。Lp1和Lp2兩個初級的漏感會影響下圖里1-2和2-3腳的電感之間的耦合，具體多少不用管，這樣兩個初級的耦合效應會在測量1-3腳電感時被算進來，實際中只需簡單測量1和3腳之間的電感量即可確定諧振電感Lr。因此這里可以把初級部分看作Lr和一個1:1的理想變壓器，其余部分則看作是2:n匝數比的理想變壓器。Ls是次級漏感，實際中對電路工作有一定影響，后面會進行分析的。變壓器和諧振電感的分解見下圖：

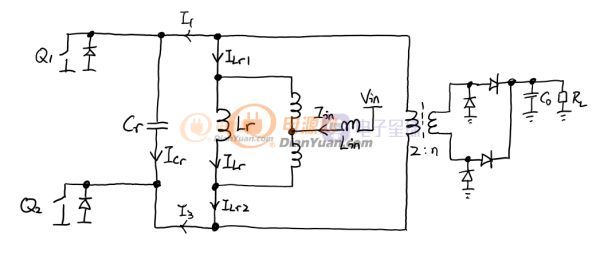
拆分之后的等效電路如下圖。注意I1和I3分別對應實際變壓器1腳和3腳的電流，Iin是ZVS的輸入電流，也是變壓器抽頭的電流。ILr, ILr1和ILr2都是實際中測不到但是有物理意義的電流。

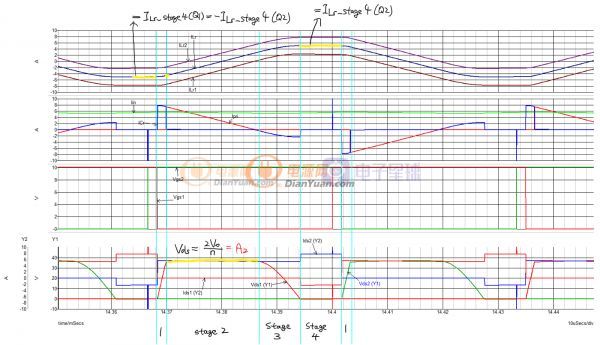
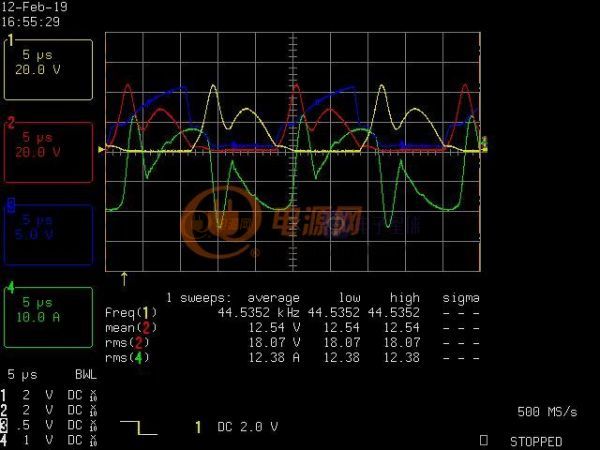
 現在可以開始正式的穩態分析了。這個電路一共有8種狀態，其中的兩兩對應(Q1 Q2開啟時分別有4種)，于是可以簡化成四種狀態，下圖展示了ZVS帶整流負載的穩態波形（看不清的話附件有高清大圖）：

在進入狀態1之前，我們假設Q1和Q2同時都在導通。什么？！做過電源的朋友都知道一般半橋和推挽最怕兩個mos管同時導通，但是這里為什么可以呢？思考一下，這里的輸入有一個大電感，在開關頻率的范圍之內，每個周期之內的輸入電流幾乎是不變的，于是Vin和輸入電感可以等效為一個電流源。電流源最怕的就是開路，因為電流沒地方去了，它會升高電壓使勁找地方讓電流維持流動，兩個管同時關閉會讓任何電流通路消失，Vds急劇升高于是就爆炸了。所以在這種電流源輸入的電源里兩個mos管一定要有共通時間，千萬不能兩個管同時關閉。因此窩懷疑Edry文章里的驅動電路可能有些不妥，他用了一個變壓器產生兩個反向的方波，可能沒有足夠的直通時間。

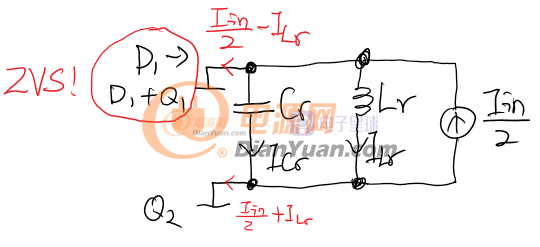
狀態1：以Q1的關斷作為開始，此時Q2已經被打開，電容和電感進行諧振，此時Q2的電流約等于輸入電流，電感和電容的電流是相等的。在狀態1開始之前一瞬間，Q1/D1上的電流為Iin/2-ILr，而Q2上電流為Iin/2+ILr。在狀態1中，LrCr諧振會導致Cr上的電壓VCr不斷上升，當VCr到達輸出電壓的變壓器初級反射電壓(Vo*4/n/n)時，狀態1結束進入狀態2。

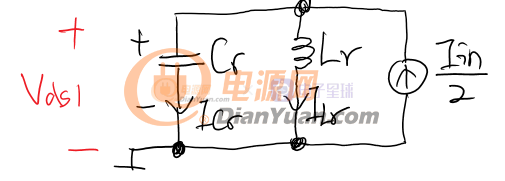
如果把Lr和自耦變壓器看作一個三端網絡，則可知ILr1+Iin=ILr2。1：1自耦變壓器將輸入電流“一分為二”，如果不看抽頭，可以發現一個端以Iin/2吸電流另一個以同樣的大小出電流，于是可以等效為Iin/2的電流源。狀態1的簡化等效電路如下。電流源的大小為輸入電流的一半：

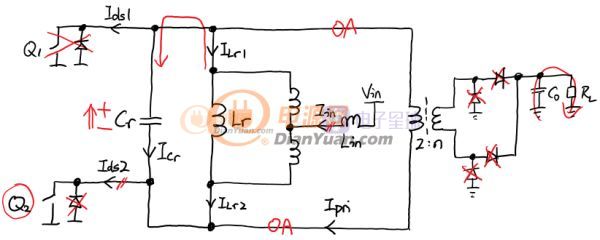
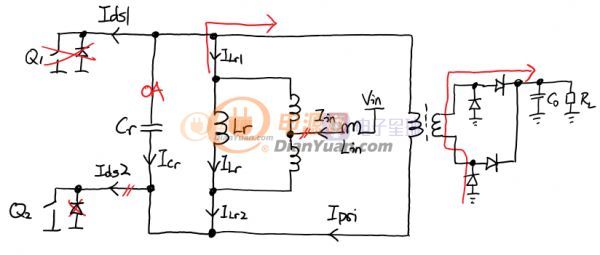
狀態2：狀態2開始之后，變壓器初級開始接管電流，Cr開始完全不通過電流，VCr被鉗位到反射電壓的水平。在這期間，輸入電流和電感電流ILr一起對負載供電，二次側整流二極管開通，從初級接收能量。有等式Ipri=ILr1=Iin/2-ILr成立。Ipri是初級電流，入下圖紅色箭頭所示。起初電感和輸入電流一起為負載供電，電感電流ILr開始下降，當ILr過零之后輸入電流為負載供電同時為Lr充能，ILr和初級電流Ipri繼續下降（實際ILr是在往另一個方向增長！），直到Ipri過零，二次側整流管關閉，進入狀態3。

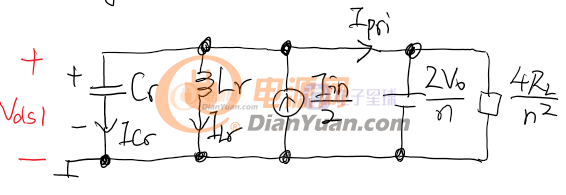
上圖是狀態2的電路圖，其簡化電路為：

狀態3：狀態3開始后，Cr再次接管ILr1（=ILr-Iin/2），此時Cr與Lr諧振，VCr開始呈正弦波規律下降，ILr1逐漸變成正的并且趨于平緩。這個狀態中Q2的電流等于輸入電流。當VCr等于0的時候，狀態3結束。

狀態3的簡化圖和狀態1是一樣的，只不過初始狀態不一樣：

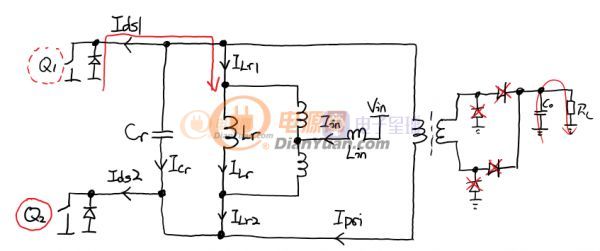
狀態4：當VCr到0V之后電感電流依然是正的（圖中從上往下），電流為了找到出路會打開新的通路。此時D1會導通。之后D1上的電流為Iin/2-ILr，而Q2上電流為Iin/2+ILr。在狀態4中，VCr一直被鉗位到接近0V，這給ZVS創造了條件（在Q2開啟的時候，Vds1=VCr），Q1可以在任何時間開啟，開啟之后電流大部分流過Q1的mos溝道少部分流過體二極管D1，狀態4維持，直到Q2關斷，然后進入狀態1的Q1鏡像版。周而復始。在Q1開始前，Lr和Lin中的電流基本保持不變。

根據這四種狀態的邊界條件，可以確定狀態1-3的時間以及功率級的變換比（M=Vo/Vin，在理想無損耗的情況下）：

 t1, t2, t3 分別對應狀態1,2,3占用的時間，狀態4所需的時間根據開關頻率不同可以改變。M是輸出電壓與輸入電壓的比值，Wr是腳諧振頻率，Zr是特征阻抗，A1，A2，A1/A2是定義的數。

之前的分析一直沒有考慮變壓器次級的漏感，這個漏感會在狀態2的時候在VCr上產生一個尖峰，原因是因為Cr和次級漏感諧振了，這個諧振的初始條件和狀態2的初始條件一樣。最終可以得到漏感引起的多余電壓峰值的公式，Lleak_sec是在次級測得的漏感大小，為初級全部短路時候讀得的電感值：

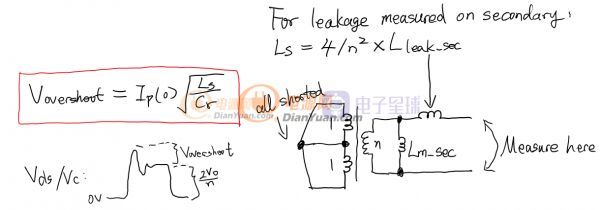
好了，到此ZVS的功率級就介紹完了。窩用的是和Edry類似的方法進行分析的，得到的結果也是基本一致的，不一致的地方主要是系數和量綱的不一致，不影響正確性。

ZVS分析！正文開始！

其實前面的這部分只能算是背景知識哦，不過有了這些知識，理解ZVS就容易多了。現在讓我們來看一下ZVS的自激電路部分，當一側的mos管的Vds開始諧振下降的時候，二極管和上拉電阻會在電壓諧振到比較低的時候逐漸開啟這另一側的mos管，而逐漸開啟的mos又會通過另一個二極管漸漸關閉這一側的mos。相對慢的Vds下降，比較大的MOS管門極電阻還有米勒平臺效應給了兩個管子一定的共通時間，完成了正常的換向。整體看來，可以認為t4也就是Q1Q2全部開通的時間極短， 也就是說狀態1，2，3占用的時間之和即等于一半頻率（因為一個完整周期每種狀態會發生兩次哦），于是能寫出下面的第一個等式，聯立二式之后即可求解fs：

很遺憾，在進行了各種嘗試之后，并沒有能夠獲得一個人能看的分析姐...fs的表達式在用了某些假設近似的情況下都復雜的要死...于是...窩想到了...圖表！沒錯！在計算機普及之前很多很難算的函數都是通過圖表來查詢的！于是上面的式子經過某些化簡處理之后，窩通過Matlab對其求數值解并制得兩張圖（matlab可以打開的圖和出圖的m文件窩放附件里（/upload/community/2019/02/05/1549347133-91782.zip）

使用方法如下：

1. 先計算三個量，分別是自然諧振角頻率，特征阻抗和歸一化的負載電阻。Lr是諧振電感，就是變壓器初級沒抽頭兩端測得的電感，Cr是諧振電容，n是匝數比，變壓器配置：1:1:n。

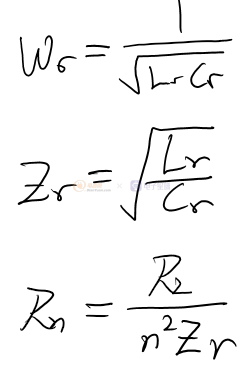
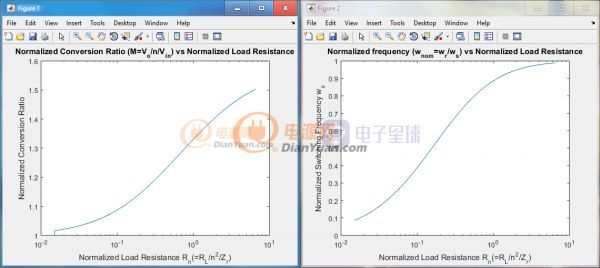
2. 通過Rn從兩幅圖中分別找到歸一化的開關角頻率(Wnom，左)和歸一化的轉換比(Mnom=M*n，右）

3. 通過如下公式計算開關頻率fs和輸出電壓Vo：

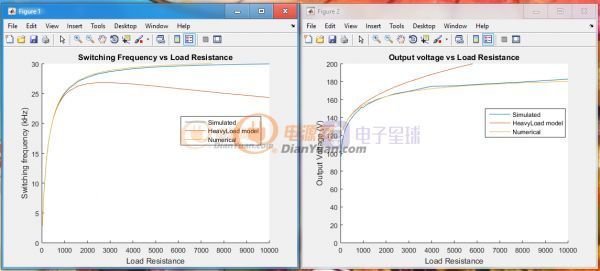
至此一個帶整流濾波輸出的ZVS在特定負載下的開關頻率和輸出電壓就可以被輕松找到了。上面的方法假設了理想的器件也就是沒有損耗，結果和現實中是會差一點點的。現在電腦很普及了，其實可以參考窩發的m文件里，給定Ro直接進行數值計算。Multisim和Simplis的仿真文件也在上面的附件里。以上的方法經過仿真驗證，精度極高：

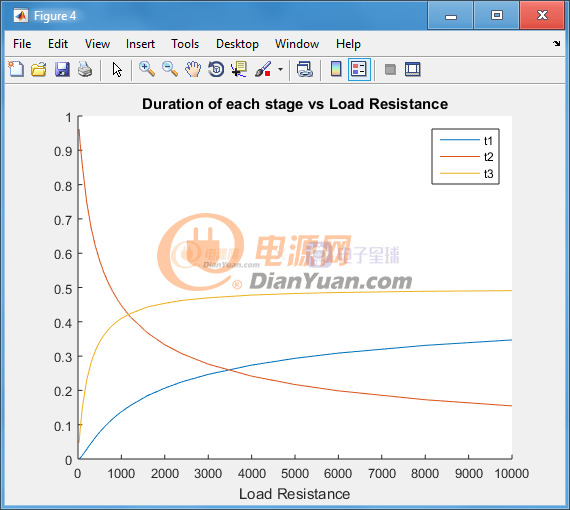
左側是開關頻率和負載的關系，右側是升壓比與負載的關系。圖表的結果是黃色線，電路仿真結果是藍色線，而這里面的HeavyLoad Model是窩算出來的一種只是適合重載情況下的分析姐，因為表達式太復雜所以就不貼出來了。下圖是狀態1,2,3在不同負載的情況下占總開關周期的比例：

在任何負載情況下，狀態3的時間都是pi/wr/2，這個是保持不變的。在負載輕的時候，狀態1和狀態3主導開關周期，在完全沒有負載的時候，狀態2不存在，此時Vds呈正弦波。在負載比較重的時候，狀態1和狀態3所占的時間會急劇降低，此時狀態2主導開關周期，Vds呈類似梯形或者矩形。另外變壓器的次級電流的波形是三角波并且不連續（上面的等效初級電流Ipri也是這個波形），在整流橋后面濾波電容前面的電流波形和臨界模式的反激變換器的次級電流基本一致。

如果這個功率電路改用它激定頻驅動，其工作頻率必須低于LrCr諧振頻率而且兩個驅動脈沖必須有一定共通，Q1Q2必須在狀態4中完成換向，如果在其他狀態換向會導致軟開關失敗。在定頻驅動下，在一定負載范圍內，變換器的次級電流與DCM的反激一致，輸出負載特性也與DCM的反激一樣，是恒功率源。

實際設計中的考慮

1. 變壓器的設計，變壓器設計是需要確保磁化電感不飽和的（只有磁化電感的磁路是在磁性材料里，而漏感的磁路在空氣里所以漏感不會飽和哦），可以根據下式進行計算：

Ae是磁芯截面積單位平方米，Bsat單位特斯拉，是磁芯飽和的磁通密度，這個根據磁芯材料來，一般是0.1-0.25T之間，不推薦往死里艸，因為在啟動一瞬間zvs是有超調的，這時候磁芯壓力會比平時大一倍。ILr_pk是最大可能的峰值的電感電流，在最低負載電阻值時計算得到。計算得到的圈數是最少的初級圈數，注意的是這是初級兩個繞組加起來的匝數，實際取比n大的一個偶數，然后中心抽頭即可。最后在給磁芯中心柱開氣息，調整到合適的電感量。變壓器初級會過高頻的AC，因此需要考慮趨膚效應。初級和次級推薦采用三明治繞法來降低漏感。

2.輸入電感的選取

輸入電感需要至少為3-4倍Lr大，其電流為有一定脈動的DC電流，但是AC成分很小，因此可以用單根粗線使勁繞，大力出奇跡。同樣的，需要確保在大的DC電流下磁芯不會飽和，因此推薦使用鐵粉芯磁環或者鐵鋁硅制作這個電感。

3.MOS管的選取

MOS管的耐壓至少為pi倍的Vin（理論上空載時Vds最高的時候），這個在別的地方有證明。同時考慮到漏感帶來的震蕩，需要相應留有富余量。漏感帶來的超壓和負載大小呈正相關，上文介紹的方法在已知漏感的情況下可以比較準的估算最大MOS的耐壓。如果不確定的話最好留有5倍輸入電壓的余量，比如12v輸入，mos管最好選擇75N75（75V）或者IRF540（100V）甚至IRFP250（200V）。

MOS管的峰值電流等于輸入電流，其有效值為輸入電流除以根號2。

4. 諧振電容的選取

電容的最大電壓就是MOS的最大電壓，大負載情況下電容的電流反而比輕載稍微少一點，因為有些電流被負載分流了，但是在狀態1和3，電流的峰值依然很高。這個電容的要求就是要ESR內阻低，電磁爐電容還是首選，其實窩在考慮，用低內阻的貼片陶瓷電容也許可以勝任，但是價格或許更高了。

5. 特征阻抗的影響

增大Cr或者降低Lr會降低特征阻抗，在同樣的諧振頻率下帶同樣負載，低阻抗的LrCr組成的ZVS能輸出更大功率。

6. 負載電阻最小能是多少？

細心的同學已經發現了，歸一化的轉換比Mnom在1到pi/2之間。pi/2對應的是空載，1對應的是臨界極重載。當然實際中會有各種損耗，所以實際的停振增益會小于1一點。假設在極重載的時候，狀態2的時間遠比狀態1和狀態3長，則超重載頻率只由狀態2決定。此時可以推出fs=wr*Rn。然后帶入Mnom=Mcritical=M/n，最后得到臨界的Rn=(1-a*a)/4/a，然后就可以算出這個ZVS的最低負載電阻值。Mcritical取值在0.95到0.97左右就行，主要是一個估計損耗的情況。當然這個方法只能大致估計停振在何時發生。不要試圖在靠近這個阻抗運行zvs，稍微不注意就會boom。

7.那推薦的負載點在哪？

負載(Po)增大會讓變壓器磁化電流(ILr)也增大，最終變壓器會飽和。計算一下泥的變壓器在這個圈數下的這個電感下的飽和電流，比它稍微小一點的磁化電流(ILr)，對應的負載電阻，就是。

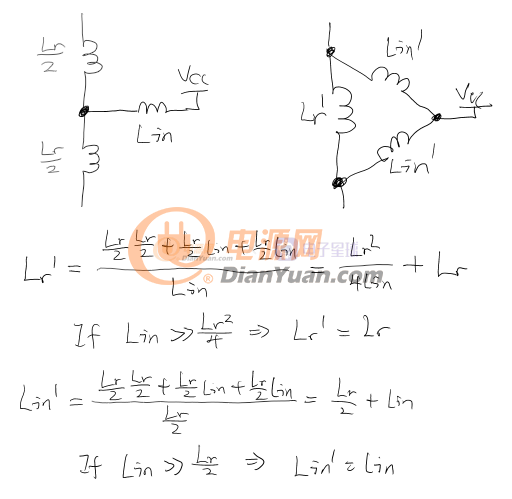
8.關于雙電感無抽頭的ZVS

把變壓器初級的Lr分配到兩個不耦合的電感上并假設輸入電感大很多:

運用三jio畫星星大法（delta to wye conversion）可以知道如果輸入電感足夠大（一般是這樣的），那么yanli12321的雙電感無抽頭zvs和帶抽頭單電感zvs是差不多的。

更新

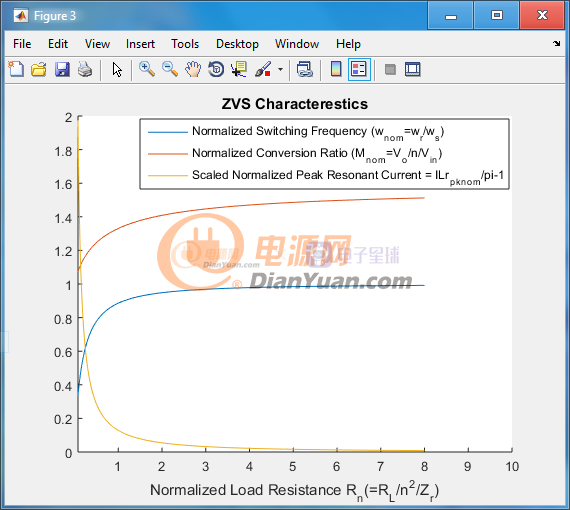
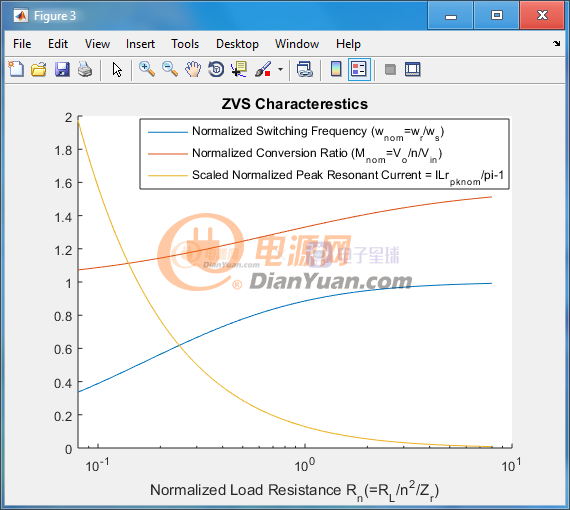
這次重新制作了ZVS特性圖，加入了估算峰值磁化電流（也是諧振峰值電流）的曲線，三條曲線合在一張圖中，后面的是x軸為指數的版本：

注意圖中的黃線代表的歸一化的峰值諧振電流是經過縮放和位移的，從圖上根據Rn讀數之后需要把讀到的數先+1再整體乘以派，這個結果就是實際的ILr_pk_nom。計算峰值諧振電感的電流可以用ILr_pk=ILr_pk_nom*Vin/Zr來得到。

下面舉一個例子說明如何用這個圖表設計ZVS自激電路。需要提供：輸入電壓Vin，在最大負載時候的輸出電壓Vo，在最大負載時的負載等效電阻Ro和自然諧振頻率fr，這個頻率也是ZVS空載的開關頻率。負載電阻Ro可以比實際的小一點，因為設計時考慮變換器是無損的。

首先選擇ZVS的工作點，ZVS的工作點這里定義為Rn的大小，Rn同時決定開關頻率，輸出電壓和峰值諧振電流(與變壓器中的磁通量成正比)。一般取歸一化諧振頻率wnom=0.6左右時的Rn值，當然0.6也可以取稍微大點或者小點。Rn確定之后Mnom和ILr_nom的值都從圖中確定了。然后帶入公式計算出所有結果：

比較大的負載就需要比較小的Zr，但是小Zr會帶來比較大的無功電流(Vin*pi/Zr，就是空載時候諧振電容的電流)。高fr需要較小的諧振電感和電容，但是Lr可能小到需要在變壓器里加很大的氣息，這樣可能會增加漏感。

結束

如果有什么錯誤/疑問/需要補充的，請在下面指出哦w

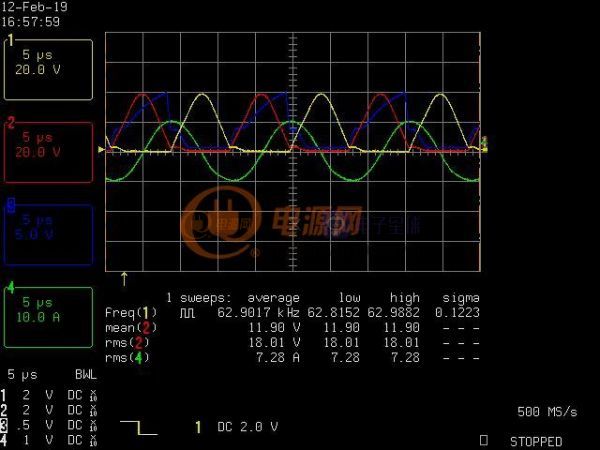
實驗驗證過程參見本貼5樓，非整流負載zvs的分析也在進行中（在另一帖更新）。